Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ ТЕПЛОВЫХ ВОСХОДЯЩИХ ЗАКРУЧЕННЫХ ТЕЧЕНИЙ ВОЗДУХА

Обухов А. Г., Баранникова Д. Д.,

§9. Особенности температурных закрученных течений воздуха в начальной стадии их формирования

Толчком в проведении цикла численных экспериментов по исследованию температурных закрученных потоков воздуха стала обнаруженная особенность их течения в начальной фазе появления закрученного потока при нагреве нижней поверхности [180].

Целью упомянутой работы был численный расчет и последующий анализ течений воздуха как сжимаемого газа со свойствами вязкости и теплопроводности в начале появления закрученного восходящего потока при локальном нагреве солнечной энергией поверхности Земли.

Математической моделью была выбрана полная система уравнений Навье-Стокса (5.1). В скалярной форме она имеет вид (5.2). Коэффициенты вязкости и теплопроводности полагались постоянными, а их безразмерные значения были равны соответственно: μ0 = 0,001; κ0 ≈ 1,46μ0.

За начальные условия были приняты функции (7.1)–(7.3). За масштабное значение расстояния было выбрано значение x00 = 105 м.

Расчетной областью был выбран прямоугольный параллелепипед с длинами сторон 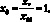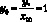и 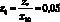 вдоль осей Ox, Oy и Oz соответственно (рис. 3.1).

Граничные условия для моделирования начальной фазы температурного закрученного течения воздуха выбирались следующим образом.

Значения плотности на боковых гранях расчетного параллелепипеда: x = 0, x = x0; y = 0, y = y0 – берутся из начального стационарного распределения покоящегося в поле силы тяжести воздуха в атмосфере Земли. На нижней грани и верхней грани z = 0, z = z0 ставится условие непрерывности потока, то есть значения плотности на этих гранях вычисляются линейной интерполяцией по значениям плотности в двух ближайших узлах расчетной сетки, находяящихся внутри расчетной области.

Граничные условия для составляющих вектора скорости газа взяты из условий непротекания для нормальной составляющей (она равна нулю на гранях расчетной области) и условиям симметрии для двух других составляющих вектора скорости (равны нулю их производные по нормали к соответствующим граням).

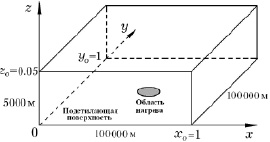
Рис. 3.1. Расчетная область численного моделирования
начальной фазы закрученного течения воздуха

Значения температуры на боковых гранях принимаются равными значениям из стационарного начального распределения покоящегося в поле силы тяжести воздуха в атмосфере Земли. На верхней грани значения температуры подчинены условию непрерывности (вычисляются линейной интерполяцией по значениям температуры в двух ближайших узлах внутри расчетной сетки). На нижней грани z = 0 температура определяется функцией

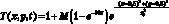, (9.1)

где M = 0,125 – коэффициент, определяющий добавку к принятому единичному масштабному значению температуры; r0 = 0,05 – безразмерное значение радиуса нагрева.

Расчеты были провведены при следующих размерных значениях плотности, скорости, расстояния и времени ρ00 = 1,2928 кг/м3,
u00 = 333 м/с, x00 = 100000 м, t00 = x00/u00 = 300,3 с, принятых за единицу масштаба. Размерное масштабное значение расстояния x00 = 100000 м соответствует размерам среднего циклона.

Шаги дискретизации по пространственным координатам Δx = Δy = 0,01, Δz = 0,005, шаг дискретизации по времени Δt = 0,001.

Значения пяти неизвестных функций с принятыми начальными условиями и поставленными краевыми условиями находятся во всех узлах прямоугольной расчетной сетки явной разностной схемой при численном решении полной системы уравнений Навье-Стокса.

Значительный интерес представляют собой результаты расчета скоростей движения частиц газа и построенные мгновенные линии тока, передающие в определенном смысле траектории частиц газа в сложном течении температурного закрученного восходящего потока.

Расчеты выявили некоторую особенность в поведении движущегося газа в начальные моменты появления температурного закрученного восходящего потока.

При постепенном нагреве плоскости z = 0 температура изменяется в цилиндрической области радиусом r0 = 0,05 от единичного, принятого за масштабное, до максимального значения.

График температуры T(x, y) в фиксированный момент времени в виде поверхности представлен на рис. 3.2.

График плотности ρ(x, y) в тот же момент времени показан на рис. 3.3.

График давления p(x, y) – на рис. 3.4.

На всех графиках по осям координат Ox и Oy отложены значения расстояния в безразмерной форме.

Из расчетов следует, что внутри области нагрева давление газа в начальные моменты времени возрастает, тогда, как за пределами области нагрева давление газа имеет пониженное значение и с увеличением расстояния от центра постепенно возрастает, и выходит на стационарные значения.

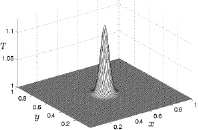
Рис. 3.2. Температура при t = 60 мин

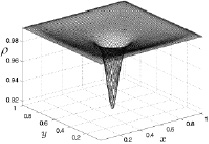
Рис. 3.3. Плотность при t = 60 мин

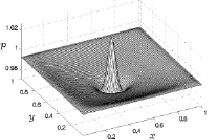
Рис. 3.4. Давление при t = 60 мин

Такое распределение давления в начальные моменты времени приводит к соответствующему поведению газа. В начале нагрева он движется в двух противоположных направлениях. Одно направление радиальное из центра нагрева к границе, а другое тоже радиальное, но противоположно направленное от периферии к границе нагрева. Такое движение газа видно на графиках x-й и y-й составляющих скорости течения, представленных на рис. 3.5 и 3.6. На осях координат Ox и Oy отложены значения расстояния в безразмерной форме.

Рис. 3.5. x-ая проекция скорости Рис. 3.6. y-ая проекция скорости

Поскольку в Северном полушарии горизонтально движущиеся частицы газа под действием силы Кориолиса отклоняются вправо от направления своего движения, то на границе области нагрева встречные потоки имеют противоположно направленную закрутку в полном соответствии с доказанными теоремами, приведенными во втором параграфе. Это приводит к появлению в этой области нескольких локальных вихревых образований с противоположным направлением вращения. Такая ситуация и наблюдается в проведенных расчетах. На рис. 3.7–3.10 показан вид сверху на мгновенные линии тока, которые в определенном смысле показывают траектории частиц газа вблизи поверхности z = 0 в различные моменты времени. На осях координат Ox и Oy отложены расстояния в безразмерной форме. Появившиеся к 500 расчетному шагу по времени (t1 ≈ 1 ч) два закрученных в противоположных направлениях вихря взаимодействуют друг с другом, перемещаясь при этом вдоль плоскости Oxy. С возрастанием времени эволюция вихрей приводит к поглощению нижним на рис. 3.8–3.10 положительно закрученным вихрем верхнего на рис. 3.8–3.10 отрицательно закрученного вихря. Это происходит, по-видимому, из-за того, что со временем радиальный поток газа, направленный к центру нагрева и закрученный в положительном направлении, постепенно начинает преобладать над противоположным потоком от центра.

Дальнейшее развитие закрученного восходящего потока при нагреве нижней поверхности идет без описанных особенностей и сопровождается ростом окружной скорости до больших значений порядка 0,2 (67 м/с) и соответствующим изменением всех газодинамических параметров.

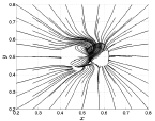
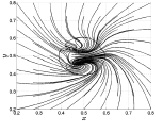
Рис. 3.7. Линии тока при t1 = 1 ч Рис. 3.8. Линии тока при t2 = 2 ч

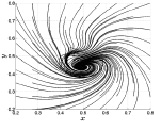
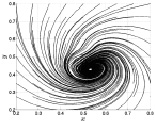
Рис. 3.9. Линии тока при t3 = 4 ч Рис. 3.10. Линии тока при t4 = 8 ч

Расчеты так же показывают, что со временем в центре теплового вихря появляется расширяющаяся до диаметра 0,15 (15000 м) свободная от мгновенных линий тока область, показанная на рис. 3.11–3.14.

Отсутствие в этой области вихря линий тока говорит о том, что внутри значительного движения газа нет, за счет больших значений окружной скорости под действием центробежной силы частицы газа выдавливаются из центральной области вихря. Другими словами, численно моделируется появление в температурном восходящем закрученном течении так называемого «глаза циклона», который, кстати говоря, перемещается в горизонтальной плоскости. Свободное перемещение «глаза циклона» и всего теплового вихря ограничивается в данной модели условием непротекания для нормальной для всех граней расчетной области составляющей скорости течения газа.

Рис. 3.11. Линии тока при t5 = 20 ч Рис. 3.12. Линии тока при t6 = 30 ч

Рис. 3.13. Линии тока при t7 = 40 ч Рис. 3.14. Линии тока при t8 = 50 ч

Фактически результаты проведенных численных экспериментов, описанных в данном параграфе, моделируют возникновение тропических циклонов при локальном нагреве солнечной энергией поверхности Земли. При этом правильно воспроизводится не только сложный нестационарный характер течений, но и соответствующие натурным наблюдениям направление закрутки, значения окружной скорости и время возрастания интенсивности тропического циклона.

Очевидно, что выявленная численными методами особенность в поведении течения газа в начальной фазе появления теплового закрученного восходящего потока будет иметь место и в других явлениях, имеющих меньшие масштабы, но с присутствием локального нагрева. Как показали дальнейшие расчеты, такое поведение течений воздуха являются характерной чертой температурных закрученных потоков, наблюдаемых в лабораторных экспериментах и в природе.