Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ ТЕПЛОВЫХ ВОСХОДЯЩИХ ЗАКРУЧЕННЫХ ТЕЧЕНИЙ ВОЗДУХА

Обухов А. Г., Баранникова Д. Д.,

§10. Результаты численного моделирования свободных тепловых вихрей, полученных в экспериментах А. Ю. Вараксина с одним локальным источником нагрева

В данном параграфе описываются результаты численного моделирования нестационарных трехмерных течений сжимаемого газа со свойствами вязкости и теплопроводности в свободных закрученных температурных потоках, инициированных локальным нагревом нижней поверхности одним источником и действием сил тяжести и Кориолиса.

Приводятся результаты нестационарных трехмерных расчетов всех газодинамических характеристик указанных потоков, результаты построения мгновенных линий тока. Установлено постепенное преобладание положительной закрутки теплового закрученного восходящего потока воздуха.

По существу, здесь предпринята попытка численно смоделировать возникновение свободных тепловых вихрей, генерируемых в лабораторных экспериментах [151–165] А. Ю. Варксина в Объединенном институте высоких температур РАН, подробно описанных в третьем параграфе.

Математическая модель для проведения расчетов также выбрана в виде полной системы уравнений Навье-Стокса (5.1), (5.2), выражающая в дифференциальной форме основные законы сохранения в движущейся сплошной среде со свойствами вязкости и теплопроводности. Постоянные коэффициенты вязкости и теплопроводности так же имеют значения: μ0 = 0,001, κ0 ≈ 1,46μ0.

Начальными условиями являются функции (7.1)–(7.3). Отличие данных начальных условий от описанных в предыдущем параграфе состоит в том, что за масштабное значение расстояния было выбрано значение x00 = 10 м, соответствующее линейным характеристикам помещения для лабораторных экспериментов [151–165].

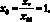
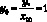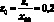Расчетная область представляется прямоугольным параллелепипедом с длинами сторон и  вдоль осей Ox, Oy и Oz соответственно (рис. 3.15).

Граничные условия и способы вычисления газодинамических характеристик на гранях расчетной области представлены следующим образом.

Значения плотности на боковых гранях параллелепипеда: x = 0; x = x0; y = 0; y = y0 – берутся из начального стационарного распределения,

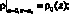
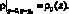
На нижней грани и верхней грани z = 0; z = z0 – ставится условие непрерывности потока.

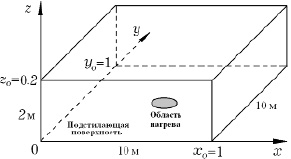
Рис. 3.15. Вид расчетной области моделирования
свободных тепловых вихрей

Это значит, что значения плотности на границе расчетной области рассчитываются линейной интерполяцией по нормали к ней из внутренних узлов расчетной области.

На боковых гранях расчетной области на значения всех составляющих векторов скорости накладываются условия непрерывности, то есть значения всех составляющих скоростей на границе рассчитываются линейной интерполяцией по нормали к ней из внутренних узлов расчетной области.

На верхней и нижней гранях заданы условия непротекания. При этом третья компонента скорости равна нулю а первая и вторая компоненты вектора скорости определяются из условия симметрии, то есть считаются из условия равенства нулю их производных по нормали к грани.

Для температуры на боковых гранях заданы значения из начального стационарного распределения

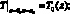
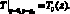
На верхней грани z = z0 заданы значения температуры из условия непрерывности.

На плоскости z = 0 температура задается функцией, моделирующей локальный нагрев подстилающей поверхности

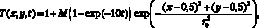(4)

где M = 0,6 – коэффициент, определяющий добавку к значению температуры, принятому за единичное масштабное значение; r0 = 0,05 – безразмерное значение радиуса нагрева. В данном параграфе приводятся результаты расчета всех газодинамических параметров при диаметре пятна нагрева 1 м и максимальной температуре в центре 460,8 К.

Расчеты были провведены при следующих размерных значениях плотности, скорости, расстояния и времени ρ00 = 1,29 кг/м3, u00 = 333 м/с, x00 = 10 м, t00 = x00/u00 = 0,03 с, принятых за единицу масштаба. Шаги дискретизации по пространственным координатам Δx = Δy = 0,01, Δz = 0,02, а шаг дискретизации по времени Δt = 0,001.

Значения пяти неизвестных функций с принятыми начальными условиями и поставленными краевыми условиями находятся во всех узлах прямоугольной расчетной сетки явной разностной схемой при численном решении полной системы уравнений Навье-Стокса.

По-прежнему, значительный интерес представляют собой результаты расчета скоростей движения частиц газа и построенные мгновенные линии тока, передающие в определенном смысле траектории частиц газа в сложном течении температурного закрученного восходящего потока.

На рис. 3.16 представлено распределение температуры на подстилающей поверхности z = 0 как функции двух пространственных переменных T(x, y) для момента времени t = 1,25 мин, для которого температура достигла своего максимального значения.

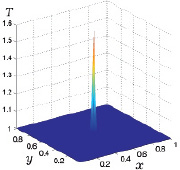
Рис. 3.16. Распределение температуры для t = 1,25 мин

По результатам расчетов отмечаются колебания максимальных значений температуры над подстилающей поверхностью относительно значения 300 °К, которые с течением времени затухают. Подобное немонотонное поведение температуры продемонстрировано на следующих четырех рис. 3.17–3.20, на которых представлены распределения температуры на высоте 0,4 м над подстилающей поверхностью для четырех фиксированных моментов времени t1 < t2 < t3 < t4.

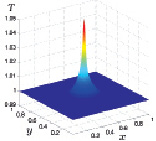
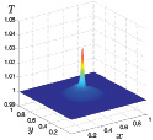
Рис. 3.17. Температура при t1 Рис. 3.18. Температура при t2

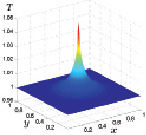
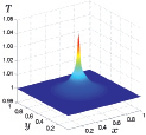
Рис. 3.19. Температура при t3 Рис. 3.20. Температура при t4

Объясняются подобные колебания, по-видимому, переходными, нестационарными процессами в изменениях газодинамических характеристик в возникающих сложных течениях газа при локальном нагреве.

Плотность газа в центре расчетной области имеет вид воронки, и форма ее существенных изменений с течением времени не претерпевает. Плотность газа, так же, как и температура совершает немонотонные периодические затухающие колебания. На подстилающей поверхности такие колебания значений плотности приближаются к минимальному значению 0,92. На высоте 0,4 м над подстилающей поверхностью значения плотности стремятся к минимальному значению 0,96. На рис. 3.21 и 3.22 представлены графики плотности.

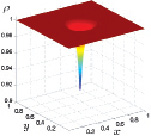
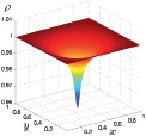
Рис. 3.21. Плотность при z = 0 Рис. 3.22. Плотность при z = 0,4 м

Из расчетов следует, что внутри области нагрева давление газа в начальные моменты времени возрастает, тогда, как за пределами области нагрева давление газа имеет пониженное значение и с увеличением расстояния от центра постепенно возрастает, и выходит на стационарные значения.

На рис. 3.23 представлен график распределения давления в фиксированный момент времени вблизи подстилающей поверхности.

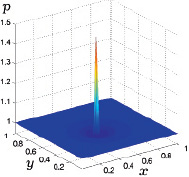
Рис. 3.23. Распределение давления газа на плоскости z = 0

Из результатов расчетов следует, что в центре расчетной области давление имеет локальный максимум, вокруг которого формируется кольцеобразная область пониженного давления. Значения давления в данной области с течением времени периодически изменяются, но постепенно выходят на стационарный режим. Периодические изменения давления проиллюстрированы на приведенных ниже рис. 3.24–3.27 при t1 < t2 < t3 < t4.

Движение газа, обусловленное изменением давления и температуры можно описать следующим образом. До 30–35 секунд газ движется от центра пятна нагрева к границам расчетной области, от 35 секунд до 60 секунд возникает противоположно направленное движения газа, а к 2,5 минутам появляется окружное движение с постепенным нарастанием значений скорости.

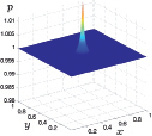
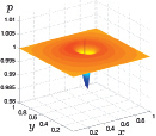
Рис. 3.24. Давление при t1 Рис. 3.25. Давление при t2

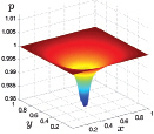
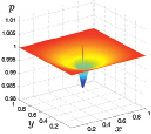
Рис. 3.26. Давление при t3 Рис. 3.27. Давление при t4

Расчет первой (x-й) компоненты скорости подтверждает описанное выше сложное движение воздуха. В начальные моменты нагрева x-ая компоненты скорости в центре области нагрева имеет противоположные по знаку значения (рис. 3.28), означающие радиальное, направленное от центра, движение газа. Это согласуется с повышенным давлением в центре области нагрева (рис. 3.24). В процессе нагрева кроме указанных противоположных по знаку значений x-й компоненты скорости появляются противоположные первым разные по знаку значения x-й компоненты скорости (рис. 3.29), означающие возникновение радиального течения газа, направленное к центру области нагрева.

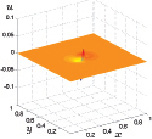
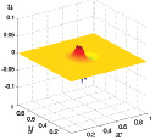
Рис. 3.28. x-ая скорость при t1 Рис. 3.29. x-ая скорость при t2

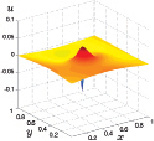
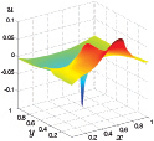
Рис. 3.30. x-ая скорость при t3 Рис. 3.31. x-ая скорость при t4

С течением времени положительные и отрицательные x-ые компоненты скорости перераспределяются в пространстве, смещаясь к соответствующим граням расчетной области (рис. 3.30). Это фактически означает начало этапа закрутки внешнего потока газа в положительном направлении.

Далее закрутка усиливается, значения x-й компоненты скорости возрастают и достигают значений 0,13 (43 м/с), что видно на рис. 3.31.

Аналогично описанному выше и поведение рассчитанной y-й компоненты скорости, графики которой в разные моменты времени представлены на рис. 3.32–3.35.

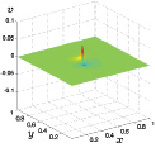
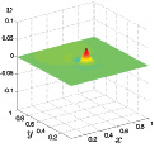
Рис. 3.32. y-ая скорость при t1 Рис. 3.33. y-ая скорость при t2

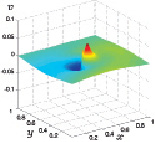
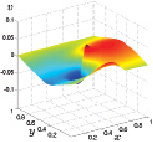
Рис. 3.34. y-ая скорость при t3 Рис. 3.35. y-ая скорость при t4

Расчеты показали, что на высоте 0,4 м от нижней плоскости вертикальная z-ая компонента скорости имеет как положительные значения, достигающие, 0,4 (133 м/с), так и отрицательные значения. Отрицательные значения третьей компоненты вектора скорости говорят о том, что вокруг восходящего потока в центре нагрева формируется нисходящее кольцеобразное течение. На рис. 3.36 приведена z-ая составляющая скорости газа в конкретный момент времени.

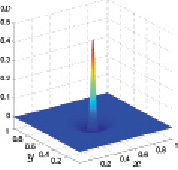
Рис. 3.36. z-ая составляющая скорости газа

В результате расчетов были построены мгновенные линии тока, которые иллюстрируют поведение газа в первоначальные моменты времени. На рис. 3.37–3.40 изображен вид сверху на мгновенные линии тока в фиксированные моменты времени вблизи поверхности z = 0.

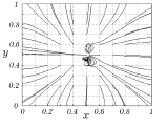
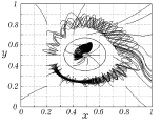
Рис. 3.37. Линии тока для t1 = 45 с Рис. 3.38. Линии тока для t2 = 1 мин

В сформировавшемся тепловом вихре четко видно кольцо диаметром 0,5 (5 м), внутри которого почти отсутствуют линии тока. Аналогичная колцеобразная структура закрученного потока наблюдается в экспериментах по генерации свободных тепловых вихрей.

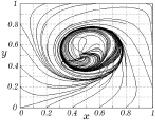
Рис. 3.39. Линии тока для t3 = 1,5 мин Рис. 3.40. Линии тока для t4 = 6,25 мин

На рис. 3.41 представлен вид под углом на линии тока вблизи поверхности z = 0 в два различных момента времени.

Рис. 3.41. Вид под углом на линии тока для двух моментов времени

В данном параграфе приведены результаты расчетов давления, плотности, температуры, всех компонент вектора скорости восходящего закрученного потока газа, вызванного локальным нагревом нижней плоскости одним источником. Построены мгновенные линии тока, передающие поведение траекторий частиц газа в сложном течении закрученного восходящего потока. Результаты расчета говорят о том, что возникающие при нагреве подстилающей поверхности течения воздуха имеют ярко выраженный сложный нестационарный характер. Возникают течения с противоположным направлением закрутки. Однако в конечном итоге преобладающим становится положительное направление закрутки всего потока.