
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
2.5. Понятие о корреляции. Повторяемость семеношения
Корреляционный анализ очень широко используется в исследовательской работе. Он позволяет оценить тесноту и достоверность разного рода связей, имеющих линейный характер. Рассмотрим его применение на примере анализа динамики семеношения сосны в два соседних года. Повторяемость уровня двух признаков семеношения – числа шишек на дереве и выхода семян из шишке – важна для понимания того, какой из них взять как основной для селекции.
Семеношение дерева определяют два элементарных биологических признака (показателя): число шишек на дереве и среднее число семян в одной шишке (выход семян). Первый определяют обычно визуально подсчетом шишек или оценкой их числа в баллах, тогда как для второго нужно извлечь семена. Как их значения повторяются по годам, и какой показатель более устойчивый?
Для оценки временной повторяемости таких меняющихся по годам показателей используют разные способы. Рассмотрим, по сути, самый универсальный из них – метод корреляции. Для примера возьмем семеношение у 30 деревьев в два соседних года. Значения показателей в первый год откладывают на горизонтальной, а второго – на вертикальной оси на так называемых «полях корреляции» (точечных диаграммах), показанных ниже для выхода семян и числа шишек на дереве (рис. 2.4).
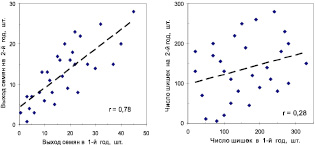
Рис. 2.4. Корреляция выхода семян (слева) и числа шишек у 30 деревьев сосны (справа) в два соседних года
Корреляция отражает тесноту прямолинейной связи и ее измеряют коэффициентом корреляции, обозначаемым буквой «r» и его значения показаны в правом нижнем углу. Справа он небольшой (r = 0,28), и связь такого уровня называют слабой; слева связь уже высокая (r = 0,78) и точки собираются более тесно у линии тренда. Для понимания того, что такое коэффициент корреляции, поясним, что он бывает близким к нулю, и тогда корреляция отсутствует (точки равномерно занимают все поле и линия тренда лежит почти горизонтально), а также близким к 1,0 и равным 0,90–0,99. В последнем случае связь приближается к функциональной, и точки лежат почти на линии тренда, а сама линия более крутая и ориентирована точно по диагонали. Корреляция бывает и отрицательной и тогда тренд имеет противоположный, чем на рисунках, наклон.
Основные требования при расчете корреляций к выборкам:
– выборка должна быть случайной;
– объем выборки должен быть не менее 15–20 пар наблюдений.
Если правила нарушить, то корреляция будет получена некорректно (смещена в большую или меньшую сторону). Для примера показано поле корреляции выхода семян у 15 деревьев неслучайной выборки, из которой исключены деревья с низким выходом семян (рис. 2.5).
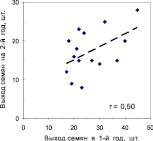
Рис. 2.5. Корреляция выхода семян у 15 деревьев сосны в два соседних года в неслучайной выборке, при отборе 50 % матерей с высоким выходом семян
Корреляция здесь сразу упала до среднего уровня (r = 0,50). Казалось бы, сравнение корреляций 0,78 и 0,50 показывает снижение в 1,56 раза, однако такое сравнение некорректно. Для сравнения их нужно возвести в квадрат, и тогда мы получим так называемый коэффициент детерминации, который показывает силу влияния одного показателя на другой. Так, в случайной выборке из 30 деревьев r2 = (0,78)2 = 0,61, а в неслучайной из 15 урожайных деревьев r2 = (0,50)2 = 0,25. То есть в первом случае сила влияния показателей первого года на показатели второго года сбора семян составила 0,61 или 61 %, а во втором случае – 25 %, что меньше в 2,44 раза, и это гораздо существеннее, чем при сравнении просто корреляций, где оно составило 1,56 раза.
Коэффициент корреляции необходимо приводить вместе с его статистической ошибкой. Ошибку корреляции m рассчитывают по формуле:
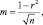 (2.6)
(2.6)
|
где r – |
коэффициент корреляции; |
|
n – |
объем выборки, шт. |
Когда такая ошибка есть, ее удваивают и быстро оценивают достоверность корреляции. Если удвоенная ошибка превышает сам коэффициент – то он недостоверен. Для более точной оценки корреляцию делят на ее ошибку: r/m и получают уже известный нам критерий t, который сравнивают со стандартом t по табл. 2.1. Используют уровень t0,95 или, если корреляции слабые, то пониженный t0,90.
Например, в нашем случае для повторяемости выхода семян r1 = 0,78 и для повторяемости урожая шишек r2 = 0,28, при числе наблюдений 30, получаем их ошибки: m1 = ± 0,07 и m2 = ± 0,17 Деление r1 и r2 на эти ошибки дает два разных критерия: t1 = 10,9 и t2 = 1,66. Для числа степеней свободы 29 в табл. 2.1 стандарт критерия t0,95 = 2,04, из чего следует, что первая корреляция достоверна, а вторая нет. Но если мы возьмем пониженный критерий t0,90 = 1,70, то второе значение t2 = 1,66 оказывается уже близко к стандарту и можно говорить о том, что повторяемость числа шишек на дереве, при корреляции r2 = 0,28 ± 0,17, может иметь место примерно в 90 % случаев, а в 10 % случаев корреляции не будет.
Выше мы кратко описали применение так называемого коэффициента корреляции Пирсона. Иногда используют и другие коэффициенты, например, ранговый коэффициент корреляции Спирмена, когда данные в количественном измерении получить трудно или невозможно. При этом данные ранжируют, и число рангов принимают равным числу пар наблюдений. Если значения равные, то их ранги усредняют. Например, по числу шишек у двух деревьев в первый год получены два одинаковых значения, равные 20 шт. (см. рис. 2.4). Они самые низкие, будут занимать ранги 1 и 2 и каждому из них присваивают ранг 1.5. Бывает и три, и четыре одинаковых значения, и тогда три или четыре ранга усредняют и всем дают одинаковые значения ранга, дробные или целые.
В тех случаях, когда связь криволинейная и линию тренда лучше описывает (аппроксимирует) не линейный, а полиномиальный или иной тип тренда, то рассчитывают так называемое корреляционное отношение, которое более точно оценивает такую связь. Но для этого нужны выборки большого объема. Бывают случаи, когда корреляция близка к нулю, а корреляционное отношение высокое. Это особенно важно для оценки силы влияния признака, когда их возводят в квадрат и получают коэффициент детерминации, о чем мы уже говорили выше.
Корреляционный анализ наиболее распространен в биометрии и имеет множество применений, которые описаны практически в любой специальной литературе (Лакин, 1973; Плохинский, 1970; Рокицкий, 1978; Тьюки, 1981). Мы же дали пояснения к нему очень кратко, делая акцент на недопущении крупных ошибок при его использовании.
