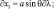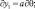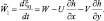Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания

МОДЕЛЬНАЯ ОЦЕНКА ЭКОЛОГИЧЕСКОЙ ОБСТАНОВКИ КОМПАНЕНТОВ ПРИРОДНОЙ СРЕДЫ С УЧЕТОМ АТМОСФЕРНЫХ ПРОЦЕССОВ
Айдосов А. , Айдосов Г. А., Заурбеков Н. С.,
2.1.2. Учет неровностей земной поверхности
Наличие реального рельефа вызывает ряд технических трудностей при представлении в конечных разностях уравнений гидротермодинамики вблизи нижней границы атмосферы. Для преодоления этих трудностей обычно вводят новую систему координат, в которой нижняя неровная поверхность переходит в плоскость (или эллипсоид, сферу). Это достигается тем, что новые координаты трансформирует поле только по одной переменной (ξ), оставляя его в остальных направлениях неизменным. Рассмотрим уравнения движения в результате преобразования координат. Для этого введем новые координаты, связанные со старыми следующими соотношениями: t1 = t; θ1 = θ; λ1 = λ; ξ1 = ξ – h(θ, λ).
Выражения градиента массовых сил в новой системе координат имеет вид:
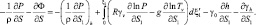
Следовательно, применение «выпрямленных» координат вводит в уравнение дополнительный член, учитывающий орографию. Хотя это слагаемое велико, но оно компенсируется в значительной степени барическим градиентом, взятым вдоль земной поверхности. Таким образом, уравнения горизонтального движения можно окончательно представить в следующем виде (используются сферические координаты θ, λ):
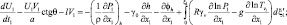 (2.13)
(2.13)
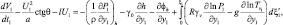 (2.14)
(2.14)
где