Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

МОДЕЛЬНАЯ ОЦЕНКА ЭКОЛОГИЧЕСКОЙ ОБСТАНОВКИ КОМПАНЕНТОВ ПРИРОДНОЙ СРЕДЫ С УЧЕТОМ АТМОСФЕРНЫХ ПРОЦЕССОВ

Айдосов А. , Айдосов Г. А., Заурбеков Н. С.,

2.1.4. Уравнения притока тепла

Для трехфазной смеси введем понятие динамического равновесия [61]. Это значит, что с точки зрения микроскопических процессов давление в каждой фазе быстро приспосабливается к некоторому общему давлению Р и температуре Т, что ни в коем случае нельзя принимать при явном рассмотрении конвективных процессов в атмосфере [92]. В макроскопическом приближении допускается, что в процессе конденсации выделяющееся тепло почти полностью отдается влажному воздуху. Это приводит к его нагреву по отношению к ненасыщенному воздуху и возникновению конвекции, при которой капли увлекаются потоком и осуществляется дополнительный адаптационный тепловой обмен между каплями
и окружающей средой. Учитывая вышесказанное, уравнение притока тепла для смеси возьмем в следующем виде:

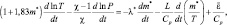(2.36)

где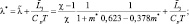

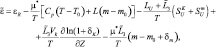(2.37)

где L – удельная теплота конденсации; Cp – удельная теплоемкость при постоянном давлении; χ – отношение теплоемкостей; ε – внешние притоки тепла.

Первый член правой части описывает изменение энергии, идущее на нагревание воздушного пара, второй – дает вклад процессов конденсации, и наконец, ε включает все остальные виды энергии.

Рассмотрим наиболее существенные из них [79, 171, 178].

1. В облачных процессах происходит постоянное смещение облачной массы с порциями свежего ненасыщенного воздуха, приводящее к изменению характеристик облачной среды. Общее изменение притока тепла за счет смешения имеет вид:

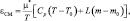(2.38)

где T0, m0 – температура и отношение смеси вовлекаемого, окружающего воздуха; μ* – коэффициент вовлечения, определяющий количество массы вовлекаемого воздуха в единице облачной массы.

2. В области отрицательных температур, переохлажденные облачные капли, замерзая, передают облачной массе тепло

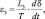
где L3 – удельная теплота замерзания. Кроме того, в результате замерзания жидкой капли баланс влаги у ее поверхности изменится. Это приведет к некоторому накоплению тепла, равному

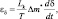
где Δm* – разность между отношениями смеси насыщения над водной поверхностью и надо льдом; Lk – удельная теплота конденсации. Объединяя эти два вида притока тепла, запишем:

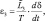(2.39)

где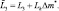

3. В процессе облачной циркуляции облачная масса может переместиться в пространство, где m0 < m*. В этом случае часть капель будет испаряться, чтобы донасытить облачную смесь. Потеря тепла за счет этого явления равна:

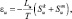(2.40)

где Lu – удельная теплота испарения; Lu 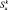и  – соответственно количество испарившихся в единицу времени крупных и мелких капель.

4. В качестве четвертого вида необходимо рассматривать приток энергии за счет конвективного переноса тепла (εk) с нижних уровней при развитии проникающей конвекции. Реализация такой формы конвективной неустойчивости и ее параметризации придается сейчас большое внимание.

Выпишем теперь уравнение притока тепла, принимая во внимание три первых дополнительных вида притока тепла:

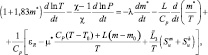
где εR включает все оставшиеся виды энергии.

Используя соотношение для 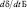, уравнение притока тепла окончательно запишется в следующем виде:

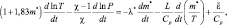(2.41)

где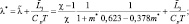

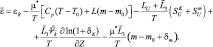
Мы видим, что форма уравнения практически не изменилась по сравнению с (2.37). Изменилось лишь содержание внешнего притока тепла, куда вошли притоки за счет вовлечения, замерзания, испарения.

Необходимо вписать еще уравнение Клаузиуса-Клапейрона:

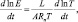(2.42)

где А – термический эквивалент работы; Rn – газовая постоянная для водяного пара,

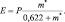(2.43)

Уравнения состояния для влажного воздуха можно записать в виде:

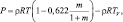(2.44)

где Т будет характеризовать температуру смеси. Если воздух насыщен, то следует положить m = m*.