Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
МОДЕЛЬНАЯ ОЦЕНКА ЭКОЛОГИЧЕСКОЙ ОБСТАНОВКИ КОМПАНЕНТОВ ПРИРОДНОЙ СРЕДЫ С УЧЕТОМ АТМОСФЕРНЫХ ПРОЦЕССОВ
Айдосов А. , Айдосов Г. А., Заурбеков Н. С.,
2.1.5. Учет в уравнениях движения неоднородности атмосферных сред
Рассмотрим движение неоднородных сред (движения влажного воздуха и мелкой компоненты, которая полностью вовлекается окружающим влажным воздухом с привлечением уравнения движения гидрометеорной части). В общем виде [43, 61] уравнения движения смеси влажного воздуха имеет вид:
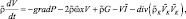(2.45)
где последний член представляет собой дивергенцию от тензора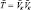 
, компоненты которого, в силу особенностей вектора 
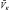, будут отличны от нуля только для вертикальной компоненты скорости. Кроме этого члена в правой части появился дополнительный член, описывающий так называемую «реактивную» силу, связанную с процессами притока и стока массы во влажной атмосфере (в данном случае за счет гравитационного оседания гидрометеоров).
Поскольку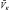 
с высотой убывает, то, видимо в большинстве случаев 
и тогда дополнительный член в уравнениях движения облачной среды будет описывать эффект, подобный внутреннему трению. В результате такого механизма атмосферные вихри, охватывающие облачные скопления, теряют свою интенсивность благодаря эффекту гравитационного оседания гидрометеорной части облаков. Если же в облаке предполагается отсутствие гидрометеоров, то естественно, рассматриваемый дополнительный эффект равно нулю.
Конвективные движения крупных облачных скоплений, помимо термического воздействия, оказывают также динамические влияния на горизонтальные потоки. Введем корректировку уравнений для горизонтальных компонент скорости за счет конвективных движений [159].
Уравнение гидростатики (третье уравнения движения) запишем следующим образом:
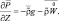(2.46)
Здесь черта означает операцию площадного осреднения, а 
– плотность облачной смеси. Последнее слагаемое запишем следующим образом:
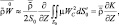(2.47)
где K – средневзвешенная по площади квадрата; S0 – кинетическая энергия вертикальных конвективных движений; μ – функция распределения кучевых облаков внутри квадрата.
Обратимся теперь к уравнениям горизонтального движения. При нахождении градиента массовых сил учтем (2.46) и (2.47):
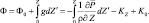
Подставляя это выражение в уравнение горизонтального движения, пологая, что K0 = 0, получим в уравнениях (2.13) и (2.14) дополнительные члены, учитывающие параметрические крупномасштабные очаги конвекции. В первом уравнении это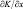 
, а во втором 
.
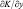Чтобы проанализировать, какой эффект оказывает присутствие этих дополнительных членов, предположим, что имеется изолированное скопление мощных кучевых облаков, находящееся в безградиентном барическом и термическом полях. Пренебрегая, ускорениями в уравнениях движения имеем
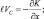(2.48)
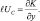
Из этих соотношений следует, что наличие больших вертикальных движений в кучевых облаках облачных скоплений мгновенно создают крупномасштабную циклоническую циркуляцию, которая «закручивает» облачное скопление, образуя характерную форму циклонического облачного вихря.
Вертикальные конвективные движения, необходимые для расчета K, вычисляются методом слоя или частиц по данным температуры и влажности. Для использования механизма «закручивания» в синоптической практике необходима предварительная статическая проработка большого объема материала, чтобы связать конвективные WC, вычисленные по единичным аэрологическим зондам, размер облачных скоплений, его форму с фактом возникновения облачного вихря, временем его формирования.