
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания

МОДЕЛЬНАЯ ОЦЕНКА ЭКОЛОГИЧЕСКОЙ ОБСТАНОВКИ КОМПАНЕНТОВ ПРИРОДНОЙ СРЕДЫ С УЧЕТОМ АТМОСФЕРНЫХ ПРОЦЕССОВ
Айдосов А. , Айдосов Г. А., Заурбеков Н. С.,
2.2.1. Уравнение для полной производной от давления и температуры в насыщенной атмосфере
Возьмем полную производную от прологарифмированного уравнения состояния, после элементарных выкладок и, разрешая относительно производной от давления и температуры, придем к системе уравнений:
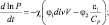 (2.49)
(2.49)
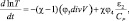 (2.50)
(2.50)
где 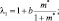
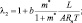
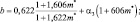
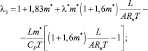
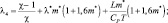
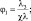
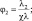
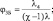
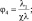
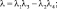
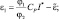
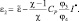
Уравнения для давления и температуры в такой форме для адиабатической, сухой атмосферы рассматривались в [44, 57].
Квазигидростатическое приближение предусматривает пренебрежение вертикальным ускорением в третьем уравнении движения, и рассмотрим уравнение неразрывности в форме
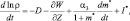 (2.51)
(2.51)
где 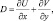 и уравнение квазистатики в следующем виде:
и уравнение квазистатики в следующем виде:
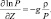
Возьмем теперь полную производную от обеих частей уравнения и получим следующее уравнение для полной производной от давления:
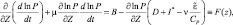 (2.52)
(2.52)
где 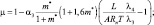
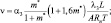
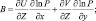
TV – виртуальная температура.
Для безоблачной атмосферы (μ = 1, v = 0) следует из (2.52):
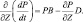 (2.53)
(2.53)
Уравнение (2.52) используется для определения 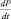 путем обычной квадратуры, удовлетворяя краевому условию на бесконечности, где
путем обычной квадратуры, удовлетворяя краевому условию на бесконечности, где 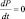 .
.
Переход в (2.53) к изобарической системе координат дает общеизвестное уравнение неразрывности
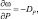
где 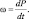
За счет μ происходит в процессе конденсации увеличение изменения давления в среднем на 5 %, если учесть убывание с высотой μ.
Оценки показывают, что все виды вкладов притоков тепла сравнимы с вкладом плоской дивергенции. Имея в виду, что v ≈ 0,2, можно грубо оценить вклад притока тепла в облачном слое величиною, оцениваемой в 10–20 % от вклада дивергенции.