Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

МОДЕЛЬНАЯ ОЦЕНКА ЭКОЛОГИЧЕСКОЙ ОБСТАНОВКИ КОМПАНЕНТОВ ПРИРОДНОЙ СРЕДЫ С УЧЕТОМ АТМОСФЕРНЫХ ПРОЦЕССОВ

Айдосов А. , Айдосов Г. А., Заурбеков Н. С.,

2.2.4. Уравнение для неадвективных изменений давления при отсутствии конденсации. Оценка роли турбулентной диффузии

Уравнения предыдущего параграфа можно автоматически трансформировать для случая влажной, но не конденсированной, сжимаемой атмосферы. Для этого необходимо положить всюду φi = 1, α3 = 0.

После несложных преобразований придем к следующей системе двух уравнений:

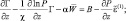
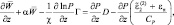(2.75)

где были введены обозначения

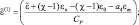
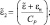
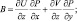
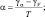
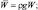
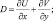
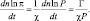
Система (2.75) является основной для определения Г – неадвективных изменений давления. Поскольку эта система явно не содержит производных по времени, то мы в дальнейшем будем называть ее диагностической частью гидродинамической модели.

Оценка вклад членов επ и εθ показывает, что εθ характеризует турбулентную передачу тепловой энергии и в атмосфере επ, εθ имеют одинаковый порядок (0,5∙10–6 с–1). Этот порядок сравним с величиной горизонтальной дивергенции, и поэтому турбулентные потоки тепла и энергии следует принимать во внимание. Члены, подобные εθ, обычно вводятся в традиционное упрощенное уравнение притока тепла.

Турбулентный поток механической энергии επ обычно не рассматривается в уравнениях гидромеханики применительно к атмосфере [55]. В рамках мелкомасштабных явлений изотропной турбулентности это оправдано в какой-то мере, что нельзя сказать о мезо- и крупномасштабных процессах, где механизм турбулентной передачи энергии играет заметную роль [38, 174].

Если в первом уравнении из (2.75) оставить только члены с горизонтальной турбулентностью, то можно написать:

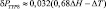(в мб/сутки). (2.76)

где 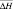и  – средние значения в тропосфере ΔH и ΔT. Символ Δ означает здесь конечно-разностный аналог оператора Лапласа.

Результаты расчетов указывают на существенную роль горизонтального турбулентного переноса механической энергии (επ) в динамике циклона, особенно заметно его роль в конечной стадии развития.