Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

МОДЕЛЬНАЯ ОЦЕНКА ЭКОЛОГИЧЕСКОЙ ОБСТАНОВКИ КОМПАНЕНТОВ ПРИРОДНОЙ СРЕДЫ С УЧЕТОМ АТМОСФЕРНЫХ ПРОЦЕССОВ

Айдосов А. , Айдосов Г. А., Заурбеков Н. С.,

2.3. Динамика вертикальных движений в облачной атмосфере

Вертикальные движения в атмосфере в процессах масштаба играет большую роль. Необходимость теоретического подхода к определению вертикальных движений вызвана отсутствием методов измерения этого метеорологического параметра. Вертикальные скорости является важным бароклинным параметром, определяющим перераспределение потенциальной и кинетической энергии в вертикальном направлении. Помимо этого, благодаря вертикальным движениям, происходит перенос водяного пара и процессы конденсации в атмосфере. Тесно связанные с конденсацией явления облакообразования и осадков, измеряемые в атмосфере, используется для оценки качества вертикальных движении. Существует обширная литература, посвященная методам расчета вертикальных скоростей [68, 77, 136, 196, 198, 204, 296]. Разнообразие подходов и методов превращает анализ этих методов в специальное исследование.

Впервые обстоятельное изложение его дано в работах Н.И. Булеева и Г.И. Марчука [42] и Хинкельмана [193], где вертикальная скорость (а точнее 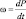) находится из решения эллиптического уравнения, в правой части которого имеются источники, вызываемые распределением адвекции вихря и температуры. Дальнейшее развитие этот метод получил в работах [44, 200].

Ф. Томпсон впервые в своей книге [299] обратил внимание, что такое балансовое соотношение (уравнение) можно построить в декартовых координатах довольно точно из системы уравнений, включающей уравнения неразрывности, притока тепла, состояния и гидростатики. Для состояния сухой атмосферы задача сводится к следующему уравнению:

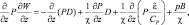(2.80)

где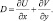

Интегрирование этого уравнения не вызывает трудностей при условиях:

z = 0; W = W0(x, y), z → ∞, p → 0. (2.81)

Похожее уравнение было получено Кимом [88] при некоторых упрощающих предположениях. В работах [165, 169] вышеприведенное уравнение обобщено на случай влажной атмосферы, в которой протекают процессы конденсации.