Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

МОДЕЛЬНАЯ ОЦЕНКА ЭКОЛОГИЧЕСКОЙ ОБСТАНОВКИ КОМПАНЕНТОВ ПРИРОДНОЙ СРЕДЫ С УЧЕТОМ АТМОСФЕРНЫХ ПРОЦЕССОВ

Айдосов А. , Айдосов Г. А., Заурбеков Н. С.,

2.3.3. Расчет вертикальных движений в многослойной облачной атмосфере

Расчет вертикальных движений в облачной среде осложнен тем, что уравнение содержит переменные коэффициенты, от которых существенно может зависеть характер решения.

В реальных условиях коэффициенты уравнения будут терпеть разрыв на границе облачной среды. Скачки коэффициентов довольно значительны, и поэтому для численной реализации уравнения необходимо применять методы «сквозного счета» [117].

Перепишем уравнение (2.52) в новых обозначениях:

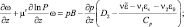(2.89)

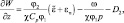(2.90)

где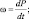

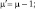
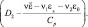
Введем дискретную систему точек, пологая ZK = KΔZK, где K = 0, 1, 2,..., M и проинтегрируем (2.89) по Z от 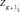до 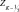основные функции, монотонно меняющиеся с высотой, внесем как среднее из-под знака интеграла, тогда получим:

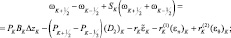(2.91)

где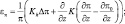

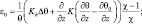
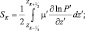
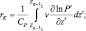
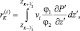(i = 1, 2).

Выразим теперь ω через W. Для этого проинтегрируем (2.90) по Z в интервале от ZK до ZK–1 из-под знака интеграла внесем величины, монотонно меняющиеся с высотой, тогда получим:

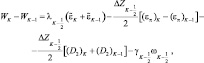(2.92)

где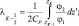

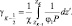
Исключением ω из (2.91) с помощью (2.92), разрешив его относительно 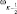, эта операция приведет нас к следующему разностному уравнению для W:

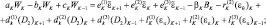(2.93)

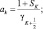
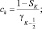
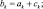
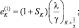
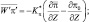
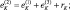
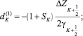
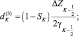
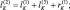
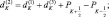
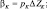
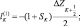
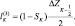
Зная по данным радиозондирования значения φi на всех высотах, можно вычислить все коэффициенты уравнения (2.93) и затем, вычислив правую часть, решить это уравнение методом прогонки.

Для некоторых целей, например, для качественных оценок, удобно записать (2.93) в матричном виде:

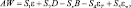
и разрешить затем относительно W. Получаемые при этом матрицы

Γe = A–1S1; Γd = A–1S2; ΓB = A–1S3

являются конечноразностными аналогами функции Грина для расслоенной облачной атмосферы.