Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

МОДЕЛЬНАЯ ОЦЕНКА ЭКОЛОГИЧЕСКОЙ ОБСТАНОВКИ КОМПАНЕНТОВ ПРИРОДНОЙ СРЕДЫ С УЧЕТОМ АТМОСФЕРНЫХ ПРОЦЕССОВ

Айдосов А. , Айдосов Г. А., Заурбеков Н. С.,

2.3.5. Параметризация конвективных процессов в численных прогнозах

Конвективные процессы являются эффективным механизмом передачи энергии из нижних слоев атмосферы в верхние. Кроме того, конвекция является механизмом стабилизации неустойчивых атмосферных процессов. Чрезмерно большую роль влажно-конвективные движения играют в теории развития тайфунов. Поскольку конденсационные процессы в кучевых облаках по пространственным и временным масштабам являются более мелкими процессами, то при расчетах крупномасштабных движений приходится использовать приемы параметризации влажной конвекции.

Ку [262], используя линейную теорию возмущений, показал, что в неустойчивой атмосфере наиболее неустойчивая мода имеет размер кучевых облаков. Эта форма неустойчивости была названа «условная неустойчивость первого рода». Ку заметил, что чисто гравитационная мода имеет также тенденцию к росту и ее пространственный размер соответствует размеру тропических циклонов. Поскольку первая мода наиболее неустойчивая, то она будет доминировать. Затем Чарней и Элиассен [231] внесли дальнейшую ясность в вопрос о сдвиге неустойчивости в сторону более крупномасштабных движений.

Используя 2-уровневую модель с учетом поверхностного трения и параметризацией нагревания кучевых облаков как функции вертикальных движений на верхней границе планетарного пограничного слоя, они показали, что наиболее неустойчивая мода имеет горизонтальный масштаб примерно 100 км (а не 1 км, как у КУ). Эта неустойчивость получила название «конвективная неустойчивость второго рода» (CISK). Этот метод требует параметризации нагревания кучевыми облаками.

Рассмотрим три существенных подхода к такой параметризации.

1. Оайама [277, 278] предложил своеобразную форму параметризации конвекции, основанную на некотором свойстве атмосферы в тропической области. Частицы из пограничного слоя всегда оказываются теплее окружающего и способны проникать до больших высот. Учитывая вышесказанное, в уравнение притока тепла вводится дополнительный приток тепла за счет конденсации εс следующего вида: εс = –ηSWp, где Wp – вертикальная скорость на верхней границе погранслоя; η – некоторый параметр, являющийся функцией пространственных координат, характеризующий степень передачи потока тепла, идущего с пограничного слоя в верхние уровни. Существует несколько способов задания η и все они мало апробированы на практических моделях. Так, в [210] предполагается использовать

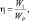(2.94)

где W1 – крупномасштабные вертикальные движения.

Эта форма задания η предполагает, что приток от конденсации целиком идет на компенсацию охлаждения за счет адебиатического подъема.

Оайама [277] использовал выражение:

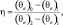(2.95)

где θe – эквивалентно-потенциальная температура.

Индекс 0 соответствует пограничному слою, 1 – окружающему пространству, а 2 – облакам.

В экспериментах по моделированию зональной экваториальной циркуляции П.Ю. Пушистов [152] применил выражение:

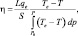(2.96)

Хайаши [248] и Т. Нитта [278] строили функции η по данным наблюдений. Задание η в форме (2.105), (2.106) применимо в тропических районах, где действует механизм проникающей влажной конвекции, начинающейся с планетарного пограничного слоя. В умеренных широтах конвективные процессы могут начаться с высот. Лежащих выше пограничного слоя, и поэтому задание η необходимо делать, исходя из других гипотез.

В этом способе конвективное нагревание распространяется до 100 миллибаровой поверхности и достигается благодаря непосредственному перемешиванию облачного и окружающего воздуха. Этот же механизм осуществляет приток влаги в окружающую атмосферу. Пограничный слой в этом способе является своего рода непрерывным источником энергии, которая перераспределяется на вышележащих уровнях.

2. Этот метод пришел из моделей по общей циркуляции атмосферы [255] и является наиболее экономичным и простым для целей длительного интегрирования. Предполагается, что перемешивание благодаря CU происходит мгновенно таким образом, что условно неустойчивая порция атмосферы «замещается» кучевым облакам, т.е. влажноадиабетической стратификацией. Требование, чтобы приспособленная энергия устойчивости Ea = gz + CPT + Lq в точке сетки была равна интегралу по вертикали от неприспособленного энергии устойчивости, является гарантией того, что не будет наблюдаться резкого изменения энергии вследствие приспособления. Приспособление осуществляется, если атмосфера устойчива и относительная влажность больше 100 %.

3. Данный метод основан на идее Аракавы [210]. Предполагается, что, если некоторый поток массы должен подниматься влажноадиабатически в облаке, то должно наблюдаться компенсационное движение вне облака. В этом методе нагревание осуществляется как за счет переноса скрытой теплоты конденсации в верхние уровни, так и за счет адебиатического нагревание окружающего воздуха на всех уровнях. Степень нагревания определяется распределением энергии устойчивости Ea. Если на нижнем уровне Ea становится больше, чем на вышележащем, то энергия передается посредством конвекции в верхние уровни в течение некоторого времени релаксации τ. Условная неустойчивость атмосферной модели удаляется в течение этого времени в сторону устойчивости, если энергия не получает снова дополнительной порции из пограничного слоя за счет конвергенции трения и турбулентных потоков.

Более совершенный подход был разработан в работе Аракавы и Шуберта [211]. Применение этого метода в глобальных моделях представляет большой интерес. В любой момент времени возникающая энергия сухо- или влажноустойчивости контролируется вертикальным турбулентным обменом таким образом, что в результате этого механизма температурная стратификация атмосферы и распределение влажности стремятся приблизить устойчивость к нейтральному состоянию. Такое предположение вполне допустимо в крупномасштабных моделях, где каждая точка представляет собой среднее состояние в окружающем квадрате размером d2, где d – горизонтальный шаг сетки. Пусть это нейтральное состояние характеризуется вертикальными распределениями 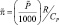и , которые связаны между собой уравнением гидростатики:

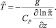(2.97)

В работе [217] нейтральную температурную стратификацию предлагается определять следующим образом:

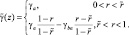(2.98)

Здесь γa, γba – сухо- и влажноадиабатические градиенты; r – относительная влажность. Значение принимается постоянным и подбирается в процессе экспериментов.

Вычислив по данным вертикального распределения T и m, находится путем интегрирования уравнения:

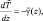(2.99)

с условием:

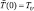
Затем из уравнения гидростатики находим:

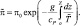(2.100)

Теперь представим, что неустойчивость реализуется путем вертикального турбулентного обмена (смотри также [232]) посредством следующего итерационного процесса:

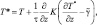
где звездочкой обозначены приспособленные величины; τ – время релаксации итерационного процесса, Это эквивалентно решению уравнения:

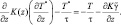(2.101)

При заданных значениях T* на верхней и нижней границах области это уравнение удобно решать методом прогонки. Если в модели температура не прогнозируется явно, то аналогичная задача должна быть решена для π*:

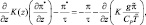(2.102)

при заданных значениях π* на границах.

Тогда приток тепла за счет конвективного нагревания определится выражением:

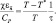
Далее считаем, что общая энергия h = CPT + gz + Lm остается консервативной в частице в пределах рассматриваемого объема. Условие консервативности заменим условием отсутствия диссипации:

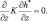(2.103)

Тогда из (2.82) следует, что

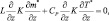
или, привлекая (2.101),

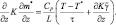(2.104)

Решение этого уравнения дает приспособленное распределение влажности (отношение смеси).

Зная теперь T* – T, из уравнения Клаузиуса-Клапейрона находим насыщающее отношение смеси, соответствующее новой, приспособленной температуре:

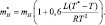(2.105)

Общее количество воды, выделившееся в результате приспособления, определяется путем следующего суммирования по слоям:

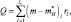(2.106)

где rl – относительная влажность.

Опять проверяется условие .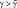

Если оно выполняется, то вся описанная выше процедура продлевается снова. Заметим, что отрицательное значение Q говорит о том, что конденсация фактически не происходила и уравнение для отношения смеси (2.104) не было необходимости решать. В этом случае находятся T* или π* по (2.101), (2.102) и 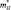 по (2.105), а m остается без изменений.