Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
МОДЕЛЬНАЯ ОЦЕНКА ЭКОЛОГИЧЕСКОЙ ОБСТАНОВКИ КОМПАНЕНТОВ ПРИРОДНОЙ СРЕДЫ С УЧЕТОМ АТМОСФЕРНЫХ ПРОЦЕССОВ
Айдосов А. , Айдосов Г. А., Заурбеков Н. С.,
2.3.6. Учет фронтальных поверхностей при расчете вертикальных движений
Методы расчета вертикальных движений позволяют довольно легко ввести в рассмотрение фронтальную поверхность. Наличие фронтальных поверхностей требует постановки соответствующих краевых условий [87, 152, 153].
Поскольку фронтальная поверхность состоит из одних и тех же частиц, то для нее имеем:
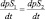или ωS1 = ωS2. (2.107)
Здесь ωS1, ωS2 – значение ω на фронтальной поверхности со стороны воздушной массы, обозначенной индексом 1 (теплая) и 2 (холодная).
Пусть далее фронтальная поверхность задана уравнением:
z = ξ(x, y, z).
Условие непрерывности нормальной составляющей скорости дает:
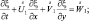
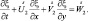
Откуда следует, что:
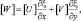(2.108)
где значок [ ] означает следующую операцию:
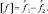
Выражения (2.118) и (2.119) определяют динамическое и кинематическое условия на фронтальной поверхности. Из (2.118) следует, что интегрирование уравнения можно проводить по всей толще атмосферы, не обращая внимания на присутствие фронтальной поверхности. Интегрирование при условии на бесконечности дает:
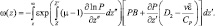(2.109)
Переходим теперь к интегрированию в массе 2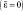 
:
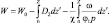(2.110)
В массе интегрирование надо вести от фронтальной поверхности до произвольной высоты Z. Но для этого необходимо знать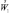 
. Записывая (2.110) при Z = ξ и подставляя в (2.108), получим:
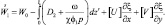(2.111)
Используя (2.111) как краевое условие, интегрирование (2.107) в пределах массы I дает:
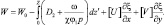(2.112)
В результате получим:
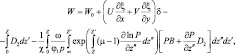(2.113)
где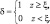 
Эффект, характеризующий скачок ветра на фронте (второй член формулы (2.113)) проявляется только над фронтальной поверхностью (в холодной воздушной массе).
Формулы (2.114) представим в конечных разностях в виде [83]:
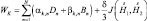(2.114)
(радиационный приток тепла не учтен).
Здесь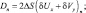 
δUx; δVy конечные разности по x и y соответственно от U, V; n – номер уровня по вертикали.
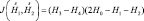
вычисляется на изобарической поверхности вдоль линии фронта. Коэффициенты αk,n и βk,n даны в табл. 29. Значение Dn и Bn определяются по картам изобарических поверхностей.
Таблица 29
Коэффициенты и для расчета вертикальных движений
в облачной и безоблачной атмосфере
|
n/k |
850 |
700 |
500 |
400 |
||
|
αk,n |
850 700 500 400 |
–0,40 0,10 0,08 0,06 |
–0,88 –0,28 0,18 0,15 |
–0,88 –0,78 –0,15 0,28 |
–0,88 –0,78 –0,15 –0,04 |
I насыщенная или ненасыщенная атмосфера |
|
βk,n |
850 700 500 400 |
1,10 1,07 0,77 0,60 |
1,33 2,32 1,66 1,33 |
1,33 2,32 3,16 2,54 |
1,33 2,32 3,16 3,28 |
II ненасыщенная атмосфера |
|
βk,n |
850 700 500 400 |
1,47 1,30 0,85 0,66 |
1,76 2,89 1,88 1,46 |
1,76 2,89 3,66 2,82 |
1,76 2,89 3,66 3,60 |
III насыщенная атмосфера |
Пользуясь формулой (2.114) и табл. 29 можно рассчитать вертикальные скорости в м∙с–1 на изобарических поверхностях 850, 700, 500 и 400 мбар. Так как αk,n слабо зависит от того, есть ли облака в данном слое или нет, то они используются для всех случаев. Если на данном уровне наблюдается конденсация (облака), то βk,n берется с третьего раздела таблицы, а если конденсация отсутствует, то берется значение со второго раздела.