
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания

МОДЕЛЬНАЯ ОЦЕНКА ЭКОЛОГИЧЕСКОЙ ОБСТАНОВКИ КОМПАНЕНТОВ ПРИРОДНОЙ СРЕДЫ С УЧЕТОМ АТМОСФЕРНЫХ ПРОЦЕССОВ
Айдосов А. , Айдосов Г. А., Заурбеков Н. С.,
2.4.4. Полуявная схема реализации прогностической модели
Неявные временные разностные схемы получили наибольшее развитие в работах советских метеорологов еще в 60-х годах, когда ограниченные возможности эвм требовали применения экономических вычислительных методов для решения прогностических уравнений. К этому направлению следует отнести работы [162, 186] с баротропной моделью, и работы садокова и немчинова [163, 288], в которых обсуждались различные варианты реализации бароклинной модели по полным уравнениям. Один из этих вариантов близко совпадает с так называемой полунеявной схемой, предложенной вычислительным центром соан, где выполнен большой ряд работ по схемам расщепления, представляющим класс неявных схем [117].
В этом параграфе будет изложена полуявная схема в интерпретации Роберта [286]. Построим ее следующим образом. Диагностическая часть модели остается без изменения – по ней находится 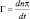 . После этого решается прогностическая часть. В работе принято, что неявно должны записываться все члены, описывающие среднее состояние атмосферы. В связи с этим обсуждается два варианта. Они отличаются формой представления π уравнениях.
. После этого решается прогностическая часть. В работе принято, что неявно должны записываться все члены, описывающие среднее состояние атмосферы. В связи с этим обсуждается два варианта. Они отличаются формой представления π уравнениях.
В первом – в уравнениях движения вместо π используется значение ln π. Во втором – используются те же параметры, что и в неявной схеме. Для удобства мы будем всюду пользоваться следующими обозначениями. Вариант модели, описанный в начале главы будем называть условно вариант S – 1, указанные выше два варианта полунеявном схемы S – 2 и S – 3 соответственно.
Рассмотрим двухшаговый временный интервал 2Δt, на котором представим уравнения следующем образом:
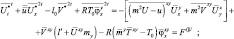
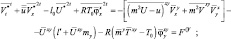
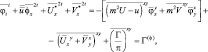
где φ = lnπ.
В последнем уравнении предполагается, что приближенно
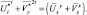 (2.133)
(2.133)
Это соотношение выполняется достаточно точно, в среднем, в принципе, оно соответствует записи:
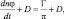
которое затем записывается на интервале 2Δt с введением центральных временных разностей с осреднением неявных членов по времени и записи явных слагаемых в центральной момент с осреднением по x, y.
Введем на рассматриваемом интервале обозначения:
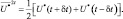
Тогда 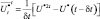 и аналогично могут быть представлены
и аналогично могут быть представлены 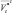 и
и 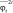 . Величины U*, V* – значения U, V в середине квадратной сетки.
. Величины U*, V* – значения U, V в середине квадратной сетки.
Левые части уравнений можно упростить, вводя новые переменные:
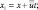 y1 = y; t1 = t.
y1 = y; t1 = t.
При этом члены типа 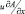 пропадут и решать задачу можно как обычно, так как при t = 0 координатные системы совпадают. В конце прогноза результаты расчета необходимо сдвинуть вдоль потока на расстояние
пропадут и решать задачу можно как обычно, так как при t = 0 координатные системы совпадают. В конце прогноза результаты расчета необходимо сдвинуть вдоль потока на расстояние  , где
, где  – средняя по всему району скорость, а t – срок прогноза.
– средняя по всему району скорость, а t – срок прогноза.
Таким образом, мы приходим к следующей системе:
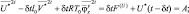 (2.134)
(2.134)
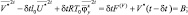 (2.135)
(2.135)
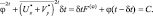 (2.136)
(2.136)
Подставляя  и
и 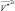 в третье уравнение, получим:
в третье уравнение, получим:
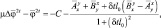 (2.137)
(2.137)
где 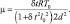
Уравнение (2.137) представляет собой разностный аналог уравнения Гельмгольца, для решения которого применимы итерационные методы. После того, как уравнение (2.137) будет решено, определяются 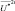 и
и 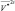 по (2.134) и (2.135), а затем прогнозируемые величины:
по (2.134) и (2.135), а затем прогнозируемые величины:
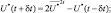
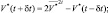 (2.138)
(2.138)
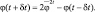
Значения U(t + δt) и V(t + δt) в основных узлах сетки находятся как средние по четырем окружающим значениям U*(t + δt) и V*(t + δt) соответственно.
На этом заканчивается цикл одного временного шага. Как показали практические расчеты, δt в этой схеме можно увеличить до 45 мин для ограниченной территории. Краевые условия использовались те же, что и для явной схемы.
Следует сделать некоторые замечания по поводу вычисления Г. В начале параграфа было сказано, что схема вычисления Г остается той же, что и для
явного метода. Поскольку для расчета надо знать π, то после каждого шага его надо определять из выражения π = exp(φ).
Это вносит определенные трудности, поэтому более экономично в схеме всюду использовать φ вместо π.
Обозначим 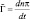 , тогда для
, тогда для  приходим к трехточечному уравнению типа (2.132), в котором:
приходим к трехточечному уравнению типа (2.132), в котором:
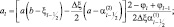
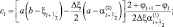
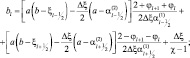
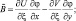
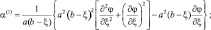
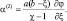
На верхней границе вместо (2.133) ставится условие:
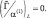
Нетрудно оценить, что 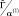 стремится на бесконечности к нулю как (b – ξ)2. Чтобы это условие было выполнено, достаточно потребовать в разностном уравнении для
стремится на бесконечности к нулю как (b – ξ)2. Чтобы это условие было выполнено, достаточно потребовать в разностном уравнении для  :
:
CL–1 = 0.
На нижней границе условие записывается следующим образом:
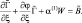
Интегрируя это выражение в пределах 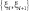 и беря l = 1, получим:
и беря l = 1, получим:
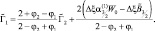 (2.139)
(2.139)
Отсюда следует, что:
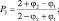
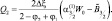
Таким образом, мы свели задачу к полунеявной разностной схеме, в которой основными параметрами являются поля скоростей и функция 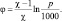 Переходим к обсуждению второго подхода. Отметим принципиальные отличия его от предыдущих вариантов. Они сводятся к тому, что во всех уравнениях рассматривается только π и его производные. В уравнениях движения член типа π представляется следующим образом:
Переходим к обсуждению второго подхода. Отметим принципиальные отличия его от предыдущих вариантов. Они сводятся к тому, что во всех уравнениях рассматривается только π и его производные. В уравнениях движения член типа π представляется следующим образом:
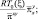
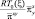 и
и 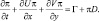 (2.140)
(2.140)
Проделывая обработку уравнений, подобно предыдущему варианту, приходим к разностной системе:
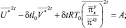
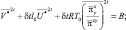 (2.141)
(2.141)
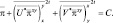
Умножая первое и второе уравнения на 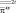 и подставляя
и подставляя  и
и  в третье уравнение, приходим к следующему уравнению для определения
в третье уравнение, приходим к следующему уравнению для определения 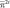 в узлах сетки:
в узлах сетки:
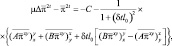
где 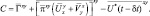
Остальные процедуры остаются прежними. Г вычисляется по схеме применяемой в явном варианте.
Из всех подходов к реализации полунеявной схемы была выбрана последняя, которая более сравнима с явной схемой и легко приспосабливается к ней с точки зрения программирования задачи.