Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
МОДЕЛЬНАЯ ОЦЕНКА ЭКОЛОГИЧЕСКОЙ ОБСТАНОВКИ КОМПАНЕНТОВ ПРИРОДНОЙ СРЕДЫ С УЧЕТОМ АТМОСФЕРНЫХ ПРОЦЕССОВ
Айдосов А. , Айдосов Г. А., Заурбеков Н. С.,
2.4.6. Учет турбулентного обмена между океаном и атмосферой
Турбулентный поток от поверхности океана определялся из выражения:
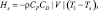(2.170)
где T1 – температура воздуха на уровне моря; Ts – температура поверхности океана.
Коэффициент сопротивления CD определялся согласно соотношениям (2.169). Затем было сделано предположение, что турбулентный поток убывает с высотой по следующему закону:
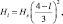(2.171)
где l – номера расчетных уровней.
Из этого закона следует, что поток тепла распространяется только до уровня l = 3 (4 км).
Напомним, что в расчетные формулы входит величина:
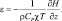(2.172)
Если мы распишем (2.172) в конечных разностях для дробных уровней, имея в виду (2.171), то тогда получим:
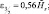
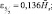
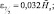
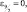(2.173)
где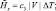 
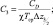
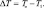(2.174)
Температура воздуха на уровне моря связана с вышележащим удобным уровнем, если известен вертикальный ее градиент. Тогда:
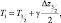(2.175)
где для γ взята в наших расчетах величина 0,006 град∙м–1.
Более точно значение ΔT можно определить, если привлечь условие теплового баланса на поверхности океана. Однако в данных экспериментах мы предполагали следующую связь:
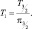(2.176)
Температура в океане в приведенных экспериментах считалась заданной в течение всего времени счета.
Как это было видно из системы уравнений (2.142)–(2.144), в ней температура не прогнозируется, а может быть вычислена по полю давления из уравнения гидростатики (2.147), которое после интегрирования в слое {zl, zl–1} имеет вид:
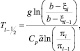(2.177)
где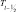 
– средняя температура слоя {zl, zl–1}.
В результате орографических и термических воздействий термическая структура модели может так измениться, что окажется неустойчивой. Для удержания модели вблизи некоторого нейтрального состояния вводится процедура приспособления. В этой процедуре решается уравнение (2.102) с краевыми условиями:
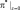– задано,
– задано. (2.178)
Выражение (2.100) можно с учетом (2.198) представить в виде:
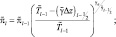(2.179)
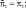
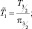
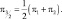
Задачу (2.102), (2.178) удобно записать следующим образом:
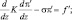
π′ = 0 при z = 0; (2.180)
π′ = 0 при z = ∞;
где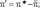 
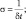
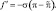
Задача (2.180) решается в точках, где хотя бы на одном уровне выполняется условие:
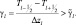(2.181)