
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания

МОДЕЛЬНАЯ ОЦЕНКА ЭКОЛОГИЧЕСКОЙ ОБСТАНОВКИ КОМПАНЕНТОВ ПРИРОДНОЙ СРЕДЫ С УЧЕТОМ АТМОСФЕРНЫХ ПРОЦЕССОВ
Айдосов А. , Айдосов Г. А., Заурбеков Н. С.,
2.4.8. Расчет радиационного притока тепла
Радиационный приток тепла для глобального варианта предполагается рассчитывать по модели «серой» атмосферы с использованием схемы Марчука [117]. Эта схема предусматривает прямое численное интегрирование уравнении радиационного переноса, в отличие от методов использующих функции пропускания [284]. Уравнения переноса длинноволновой радиации представляются в конечных разностях относительно дивергенции радиационных потоков 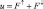 , где
, где 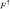 ,
, 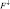 – радиационные потоки снизу и сверху, соответственно. Получающееся при этом разностное уравнение имеет трехточечную структуру и решается методом обычной прогонки. Коэффициенты уравнения зависит от коэффициентов поглощения и плотности таких субстанции как водяной пар, водные капли, озон, углекислый газ.
– радиационные потоки снизу и сверху, соответственно. Получающееся при этом разностное уравнение имеет трехточечную структуру и решается методом обычной прогонки. Коэффициенты уравнения зависит от коэффициентов поглощения и плотности таких субстанции как водяной пар, водные капли, озон, углекислый газ.
Прямая солнечная радиация вычисляется из уравнения:
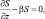 (2.184)
(2.184)
где 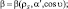 ρs – плотность поглощающих субстанции; α′ – коэффициент поглощения; υ – зенитный угол Солнца.
ρs – плотность поглощающих субстанции; α′ – коэффициент поглощения; υ – зенитный угол Солнца.
При наличии облачности, предполагалось, что солнечная радиация полностью поглощается в облачном слое. После определения u и S находится радиационный приток тепла на каждом уровне l:
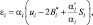
где B* = σT4; σ – постоянная Стефана-Больцмана; αl – суммарный коэффициент поглощения длинноволновой радиации.
Указанная модель расчета u была проверена на материале сравнительных наблюдений различных типов радиометрозондов, опубликованных ВМО [243]. Там же приведены расчеты длинноволнового излучения по более точной, спектральной модели [284]. В расчетах по схеме Марчука были сделаны следующие предположения:
1. Вертикальное распределение озона задано климатическим.
2. Плотность CO2 рассчитывается по формуле:
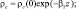
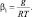
3. Распределение плотности водяного пара вычислялось следующим образом:
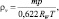
где RW – газовая постоянная для водяного пара; m – отношение смеси.
4. С помощью диаграммы определялись границы облачного слоя и плотность водных капель находилась из предположения, что вся влага в облачном слое конденсируется [251].
5. S0 = 1,98 кал∙см–1мин–1.
В модели «серой» атмосферы важное место занимает подбор оптимальных значений коэффициентов поглощения.
В результате большого числа экспериментов были подобраны средние коэффициенты поглощения для четырех поглощающих субстанции (пар, вода, озон, CO2). Для αc имеет место соотношение:
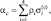
где ρi – плотность i-й поглощающей субстанции; ρi 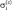 – соответствующий ей массовый коэффициент поглощения.
– соответствующий ей массовый коэффициент поглощения.
Для 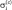 были выбраны следующие значения: водяной пар
были выбраны следующие значения: водяной пар 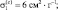
водные капли 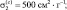 озон
озон 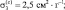 CO2
CO2 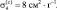
В наших расчетах облачные слои практически учитывались интегрально и конечно, не ставилась цель получить тонкие структуры потоков радиации в окрестностях облаков и они могут быть подкорректированы соответствующим подбором коэффициентов рассеяния αs.
Таким образом, следует сделать вывод о принципиальной пригодности интегральной модели для описания радиационной структуры атмосферы. Учитывая ее относительную простоту, можно надеяться на эффективность использования такой модели численных схемах долгосрочных прогнозов погоды.
Таблица 31
Сравнение V в кал∙см2∙мин–1 для многоуровневой (А) и 5-уровневой (В) радиационной модели
|
H, км |
A – для первого примера |
В – для первого примера |
А – для второго примера |
В – для второго примера |
|
22,0 |
0,290 |
0,283 |
0,309 |
0,309 |
|
11,0 |
0,312 |
0,307 |
0,410 |
0,412 |
|
5,9 |
0,514 |
0,518 |
0,506 |
0,502 |
|
2,5 |
0,726 |
0,734 |
0,677 |
0,695 |
|
0,58 |
0,800 |
0,800 |
0,790 |
0,794 |
|
0 |
0,798 |
0,800 |
0,800 |
0,794 |
Для того чтобы выяснить, насколько существенно скажется на результатах вертикальное разрешение, были проведены расчеты по многоуровневым и 5-уровневым данным модели атмосферы. Сравнение двух случаев (табл. 31) показало, что различия несущественны, и 5-уровневая модель достаточно хорошо описывает вертикальное распределение u .