
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания

МОДЕЛЬНАЯ ОЦЕНКА ЭКОЛОГИЧЕСКОЙ ОБСТАНОВКИ КОМПАНЕНТОВ ПРИРОДНОЙ СРЕДЫ С УЧЕТОМ АТМОСФЕРНЫХ ПРОЦЕССОВ
Айдосов А. , Айдосов Г. А., Заурбеков Н. С.,
3.1.1. Исходная система уравнений локальных атмосферных процессов
Согласно изложенному выше из второго раздела данной работы возьмем следующие уравнения в виде:
– движения:
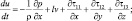 (3.1)
(3.1)
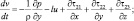 (3.2)
(3.2)
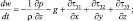 (3.3)
(3.3)
– неразрывности:
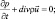 (3.4)
(3.4)
– состояния (Клайперона):
p = ρRT; (3.5)
– притока тепла:
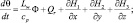 (3.6)
(3.6)
– удельной влажности:
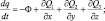 (3.7)
(3.7)
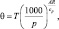 (3.8)
(3.8)
где 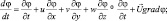 φ = (u, v, w, θ, q).
φ = (u, v, w, θ, q).
Скорость образования жидкой фазы Ф с точностью до турбулентных членов представим в виде [39, 104].
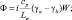 (3.9)
(3.9)
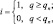
где γa – сухоадиабатический градиент; γa, γb – влажноадиабатический градиент, который определяется формулой:
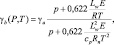 (3.10)
(3.10)
где t – время; u, v, w – компоненты вектора скорости ветра в направлений декартовых координат x, y, z соответственно; 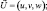 T – температура; θ – потенциальная температура; p – давление; q – удельная влажность; ρ – плотность; R – универсальная газовая постоянная; Lw – скрытая теплота конденсации; cp – удельная теплоемкость воздуха при постоянном давлении; Qr – радиационная составляющая притока тепла; A – термический эквивалент работы; g – ускорение свободного падения; l – параметр Кориолиса; τi,j, (
T – температура; θ – потенциальная температура; p – давление; q – удельная влажность; ρ – плотность; R – универсальная газовая постоянная; Lw – скрытая теплота конденсации; cp – удельная теплоемкость воздуха при постоянном давлении; Qr – радиационная составляющая притока тепла; A – термический эквивалент работы; g – ускорение свободного падения; l – параметр Кориолиса; τi,j, (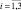 ,
, 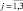 ) – тензор вязких напряжений Рейнольдса; Hi, Qi,
) – тензор вязких напряжений Рейнольдса; Hi, Qi, 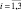 – потоки тепла и влаги в направлениях x, y, z соответственно. Вид слагаемых τi,j, Hi, Qi конкретизируем отдельно.
– потоки тепла и влаги в направлениях x, y, z соответственно. Вид слагаемых τi,j, Hi, Qi конкретизируем отдельно.
Решать задачи мезометеорологии непосредственно с помощью системы (3.1)–(3.8) нецелесообразно в связи с тем, что, во-первых, система кроме интересующих нас локальных атмосферных процессов описывает крупномасштабные процессы, звуковые волны. Во-вторых, не все члены имеют одинаковый порядок, а некоторые нелинейные члены могут быть без ущерба для физического смысла и точности линеаризованы.
В данном случае такими членами являются:
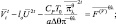
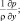
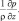
Для линерализации этих членов, введем функцию [37, 104], пропорциональную давлению:
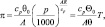 (3.11)
(3.11)
где Θ0 – среднее значение потенциальной температуры.
Используя уравнения состояния, определение потенциальной температуры и функции, получим:
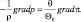 (3.12)
(3.12)
Учитывая, что 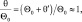 так как
так как 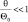 , систему уравнений (3.1)–(3.3) приведем к виду:
, систему уравнений (3.1)–(3.3) приведем к виду:
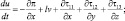 (3.13)
(3.13)
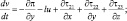 (3.14)
(3.14)
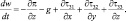 (3.15)
(3.15)
Для того чтобы получить согласованную систему для локальных атмосферных движений, представим метеорологические поля в виде
p = P + p′; π = Π + π′; ρ = R + ρ′; T = T + T′; θ = Θ + θ′. (3.16)
Здесь большими буквами обозначены фоновые поля, а штриховыми – отклонения.
Подставляя (3.16) в (3.6), (3.7) и (3.13)–(3.15) и отбрасывая малые величины, которые появляется в последствии предположения, что T′ << T, p′ << P, π′ << Π, 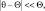 а затем, вычитывая из получившихся уравнений соответствующие уравнения для фоновых полей, получим искомую систему уравнений локальных атмосферных процессов. Для построения уравнений в возмущениях потребуем, чтобы фоновые поля с точностью до малых слагаемых удовлетворяли исходной системе (3.1)–(3.7), кроме того, предполагая временно-пространственные колебания ρ незначительными, получим окончательную систему уравнений:
а затем, вычитывая из получившихся уравнений соответствующие уравнения для фоновых полей, получим искомую систему уравнений локальных атмосферных процессов. Для построения уравнений в возмущениях потребуем, чтобы фоновые поля с точностью до малых слагаемых удовлетворяли исходной системе (3.1)–(3.7), кроме того, предполагая временно-пространственные колебания ρ незначительными, получим окончательную систему уравнений:
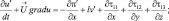 (3.17)
(3.17)
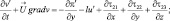 (3.18)
(3.18)
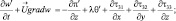 (3.19)
(3.19)
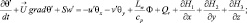 (3.20)
(3.20)
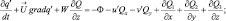 (3.21)
(3.21)
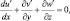 (3.22)
(3.22)
где 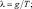 S = γa – γ – параметры конвекции и температурной стратификации; γ – вертикальный градиент стандартной атмосферы;
S = γa – γ – параметры конвекции и температурной стратификации; γ – вертикальный градиент стандартной атмосферы; 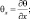
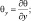
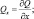
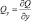 – горизонтальные градиенты фоновой потенциальной температуры и удельной влажности.
– горизонтальные градиенты фоновой потенциальной температуры и удельной влажности.
Отметим, что систему (3.17)–(3.22) можно в некоторых случаях упростить следующим образом. Если горизонтальные процессы рассматриваемых процессов много больше вертикальных и нет интенсивных источников возмущений, способных привести к мощным вертикальным ускорениям, то в уравнении (3.19) можно пренебречь операторами переноса и турбулентного переноса, а также производной по времени. Тогда уравнение (3.19) примет вид:
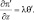 (3.23)
(3.23)
В дальнейшем, для численного расчета будем использовать уравнения гидротермодинамики в квазистатистическом приближении.