Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

МОДЕЛЬНАЯ ОЦЕНКА ЭКОЛОГИЧЕСКОЙ ОБСТАНОВКИ КОМПАНЕНТОВ ПРИРОДНОЙ СРЕДЫ С УЧЕТОМ АТМОСФЕРНЫХ ПРОЦЕССОВ

Айдосов А. , Айдосов Г. А., Заурбеков Н. С.,

3.1.2. Постановка краевых и начальных условий для системы уравнений гидротермодинамики

Одним из важных аспектов решений задач пограничного слоя атмосферы является постановка математически корректных и физически непротиворечивых краевых и начальных условий для системы уравнений гидротермодинамики (3.17)–(3.23). Постановка краевых и начальных условий во многом зависит от особенностей каждой конкретной задачи. Поэтому рассмотрим лишь некоторые общие замечания относительно условий для скорости, температуры и влажности.

Начальные условия при t = 0 в моделях рассматриваемого типа задаются по данным измерений, и таким образом относятся к числу входных параметров. Однако на практике получение детальной физической информации о начальных мезомасштабных полях затруднено, поэтому, для проведения числовых расчетов можно положить:

u′ = 0, v′ = 0, θ′ = 0, q′ = 0 при t = 0. (3.24)

В этом случае решение задачи при небольших значениях t ∈ [0, T] будет описывать адаптацию метеорологических полей к условиям, когда в процесс включается турбулентность.

При решении конкретных практических задач в общем случае целесообразно задавать начальное условие при t = 0 в следующем виде:

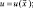
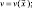
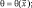
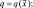
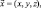(3.24а)

где u, v, θ, q – определяются из результатов измерений в реальной атмосфере. Учитывая, что информация о полях метеоэлементов поступает от сети станций, расположенных в нерегулярной области, требуется предварительно провести процедуру восстановления значений метеоэлементов в узлах регулярной сети. Aлгоритм восстановления полей по данным измерений описан в [34, 48, 57].

В качестве краевых условий по горизонтали примем:

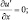
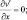
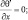
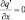при x = ±X; (3.25)

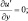
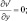
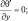
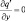при y = ±Y. (3.26)

Для того, чтобы условия (3.25)–(3.26) не противоречили данным о рельефе δ(x, y) и температуре почвы Ts(x, y), будем задавать функции δ и Ts, так, чтобы в некоторой малой ε окрестности границ ±X, ±Y исчезали неоднородности рельефа и температуры подстилающей поверхности:

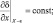
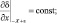
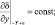(3.27)

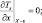
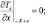
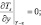
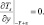
Постановка условий для (3.25)–(3.27) вызвана отсутствием информации о реальных мезометрологических полях.

Наряду с условиями (3.25)–(3.26), будем рассматривать условия, определяющие выход процессов, происходящих внутри области на режим фонового потока. Эти условия могут быть записаны следующим образом:

u = UΦ; v = VΦ; θ = ΘΦ; q = QΦ при x = ±X, y = ±Y. (3.28)

Теперь рассмотрим постановку краевых условий по вертикальной координате z. Естественно, можно предположить, что достаточно большой высоте происходит затухание возмущений метеорологических элементов, т.е.

u′ = 0; v′ = 0; θ′ = 0; q′ = 0; w′ = 0 при z = H = const, (3.29)

которое соответствует предположению, что движение ограничено сверху неподвижной плоскостью.

В некоторых задачах пограничного слоя атмосферы вместо (3.29) используются более реальные условия:

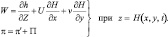(3.30)

Неизвестная функция H(x, y, t) описывает незакрепленную поверхность верхней воздушной массы. Первое условие (3.30) является условием обтекания идеальной жидкостью криволинейной поверхности.

При z = δ(x, y) в качестве краевых условий примем:

u = 0; v = 0; 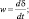θ′ = f(x, y, t); 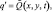(3.30а)

где функции f(x, y, t), 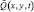пока считаются заданными величинами.