
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания

МОДЕЛЬНАЯ ОЦЕНКА ЭКОЛОГИЧЕСКОЙ ОБСТАНОВКИ КОМПАНЕНТОВ ПРИРОДНОЙ СРЕДЫ С УЧЕТОМ АТМОСФЕРНЫХ ПРОЦЕССОВ
Айдосов А. , Айдосов Г. А., Заурбеков Н. С.,
3.1.4. Замыкание системы уравнений гидротермодинамики относительно оператора турбулентного обмена
Система уравнений (3.17)–(3.23), описывающая динамику пограничного слоя атмосферы, является незамкнутой относительно величин 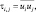 представляющих собой тензор вязких напряжений Рейнольдса. В настоящее время уже хорошо известно, что роль этих напряжений в динамике осредненного течения очень велика и пренебречь ими никак нельзя.
представляющих собой тензор вязких напряжений Рейнольдса. В настоящее время уже хорошо известно, что роль этих напряжений в динамике осредненного течения очень велика и пренебречь ими никак нельзя.
При самых ранних попытках решить систему уравнений гидротермодинамики турбулентные напряжения 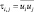 представлялись по аналогии с вязкими напряжениями в ньютоновской жидкости, только коэффициент пропорциональности перед градиентом скорости задавался большим и назывался коэффициентом турбулентного обмена или турбулентной вязкости:
представлялись по аналогии с вязкими напряжениями в ньютоновской жидкости, только коэффициент пропорциональности перед градиентом скорости задавался большим и назывался коэффициентом турбулентного обмена или турбулентной вязкости:
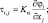 φi = (u, v, w)i. (3.56)
φi = (u, v, w)i. (3.56)
В ранних работах, начиная с работы Экмана [22], уравнения решались с постоянными или как-либо априорно заданными коэффициентами турбулентного обмена. Решение системы уравнений гидродинамики при Kα = const показывает, что оно не согласуется с некоторыми физически ясными свойствами интересующего нас течения, даже если толщину пограничного слоя рассматривать как заданный внешний параметр. Недостаток решения заключается в том, что из него следует пропорциональность сдвига ветра сдвигу скорости геострафического ветра при сколь угодно больших значениях Kα.
Следующим этапом явились исследования Е.Н. Блиновой и И.А. Кибеля [36, 83], М.Н. Юдина [204], в которых предложено выражать некоторые характеристики профиля коэффициенты турбулентного обмена через характеристики профиля средней скорости.
Далее А.С. Монин [135, 136] предложил для замыкания использовать уравнения баланса турбулентной энергии, и вытекающие из гипотезы приближенного подобия Колмогорова некоторые соотношения [92].
Суть моделей, основанных на замыкании второго порядка состоит в том, что вторые моменты, а именно напряжения Рейнольдса и потоки скалярных
субстанции не апроксимируются посредством приближения турбулентной диффузии, а сохраняются как неизвестные параметры. Для замыкания задачи вводятся уравнения вторых моментов. Моменты из третьего порядка, которые появляются в уравнениях, апроксимируются на основании некоторых предположений подобия.
В данной работе, следуя [85, 87, 98, 112], симметричный тензор напряжения τi,j, представим в виде функции, зависящей от тензора деформации Di,j среднего движения следующим образом:
τi,j = KMDi,j, i, j = 1, 2, 3, (3.57)
где 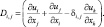 (3.58)
(3.58)
Поток тепла определим по формуле:
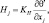 j = 1, 2, 3, (3.59)
j = 1, 2, 3, (3.59)
где KM, KH – параметры кинематической вязкости и диффузии.
Для определения пространственно-временных изменений параметра KM будем пользоваться формулировкой схемы замыкания:
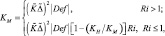 (3.60)
(3.60)
где 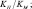
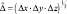 – объем элементной расчетной ячейки сеточной области;
– объем элементной расчетной ячейки сеточной области;  – числовая константа. Деформацию Def определим по формуле:
– числовая константа. Деформацию Def определим по формуле:
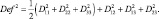 (3.61)
(3.61)
Число Ричардсона Ri представим в следующем виде [115]:
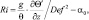 (3.62)
(3.62)
где 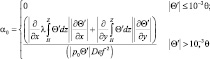
дополнительное слагаемое α0 имеет стабилизирующий характер. Поскольку при наличии сильной орографической и термической неоднородности могут возникнуть большие температурные градиенты, введение параметра α0 способствует погашению мелкомасштабных колебательных процессов.
В численных расчетах значения безразмерной константы  брались из интервала 0,2–0,4 .
брались из интервала 0,2–0,4 .
При проведении численных расчетов в квазистатистическом приближении применяется несколько упрощенное представление турбулентных слагаемых в виде:
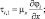
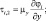
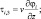
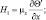
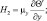
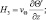 (3.63)
(3.63)
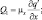
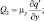
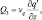 i = 1, 2, φ = (u, v),
i = 1, 2, φ = (u, v),
где коэффициенты вертикального турбулентного обмена vu, vθ, vq определяются из уравнения баланса энергии турбулентности. Такое упрощение имеет смысл, поскольку в нижних слоях атмосферы одним из существенных факторов, влияющих на турбулентную структуру пограничного слоя атмосферы, являются вертикальные градиенты скорости ветра и температуры, которые на 1–2 порядка превосходят горизонтальные градиенты.
В дальнейшем, поскольку горизонтальные размеры рассматриваемой области намного больше, чем вертикальные, ограничимся рассмотрением двухмерного тензора, а вертикальный коэффициент турбулентного обмена vu определим из решения уравнения баланса турбулентной энергии.