Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

МОДЕЛЬНАЯ ОЦЕНКА ЭКОЛОГИЧЕСКОЙ ОБСТАНОВКИ КОМПАНЕНТОВ ПРИРОДНОЙ СРЕДЫ С УЧЕТОМ АТМОСФЕРНЫХ ПРОЦЕССОВ

Айдосов А. , Айдосов Г. А., Заурбеков Н. С.,

3.2.3. Численный метод

Рассмотрим теперь численную модель переноса и диффузии примеси в пограничном слое атмосферы с характерным горизонтальном масштабом порядка 100–200 км на фоне локальных атмосферных процессов. Все необходимые значения метеорологических полей и турбулентные характеристики определим из модели гидротермодинамики, описанной в разделах 2, 3 п. 1,2.

Для численного интегрирования метод расщепления, позволяющий систему четырехмерных уравнений в частных производных расщепить на три системы двумерных уравнений в переменных (x, t), (y, t), и (z, t). Каждая из этих систем интегрируется последовательно на каждом временном шаге, и полученное в конце цикла решение аппроксимирует исходную систему уравнений (3.64). Таким образом, дело сводится к интегрированию следующей системы:

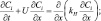(3.67)

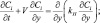(3.68)

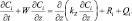(3.69)

Если ввести обозначение Tx, Ty и Tz для численных аппроксимаций операторов транспорта примесей в направлениях X, Y, и Z соответственно, Тс для оператора химической трансформации, и для источников выбросов, то полное решение может быть получено в виде:

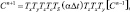(3.70)

где ∆t – шаг по времени; n – текущий номер временного слоя.

Операторы Tx, Ty, и Tz в свою очередь также расщепляются на адвективные и диффузионные компоненты, т.е. Tx = (Tx)a(Tx)d, Ty = (Ty)a(Ty)d, Tz = (Tz)a(Tz)d.

Рассмотрим отдельно каждый этап решения для трех основных базовых операторных уравнений, соответствующих адвекции, диффузии и химической трансформации, с помощью которых согласно (3.70) определяется результирующее решение в момент времени n∙∆t.

а) Решение адвективного уравнения основано на использование явной разностной схемы со вторым порядком аппроксимации, обладающей свойством консервативности для массы. Эта схема имеет вид:

(3.71)

где 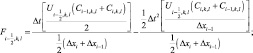(3.72)

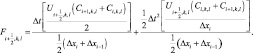(3.73)

Для предотвращения значительных технических ошибок и размывания «пиков» концентраций, а также сохранения положительных значений переменных Cikl используется коррекция потоков [33]:

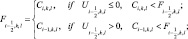(3.74)

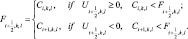(3.75)

Аналогичные соотношения могут быть получены и для компонент y, Z:

б) разностные схемы для решения диффузионного уравнения строятся в зависимости от координатных направлений. Горизонтальной плоскости доминирует адвекция, поэтому можно использовать обычную трехточечную явную схему:

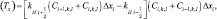(3.76)

Для направления Z, с целью уменьшения ограничения на выбор используется неявная схема Кранка-Никольсона [33].

в) этап химической трансформации сводится к решению на интервале a∆t в каждой сеточной точке моделируемой области системы обыкновенных дифференциальных уравнений вида:

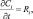
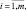(3.77)

где Ri определяется в зависимости вида (3.65).

В силу отмеченной жесткости системы (3.77), для решения следует использовать полунеявные методы [38]. Один из простейших методов такого класса реализуется следующим образом. Пусть концентрации всех примесей (исключая i) известны (либо из предыдущего шага, или уже вычислены на текущем шаге). Тогда решение (3.77) можно аппроксимировать формулой:

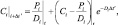(3.78)

исходя из соотношения:

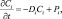(3.79)

где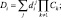

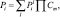
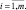
Предлагаемый алгоритм численного интегрирования основан на подразделении участвующих в химических реакциях примесей на две группы. Первую группу (возможно, пустую) составляют короткоживущие примеси типа OH, H2O2. Другую группу составляют оставшиеся долгоживущие примеси (SO2, CO2 и т.д.). Для определения концентраций примесей группы используется система алгебраических уравнений, полученная из псевдо-стационарной аппроксимации соответствующих правых частей в (3.79):

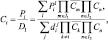(3.80)

где I1, I2 – множество индексов соответствующих короткоживущим и долгоживущим примесям, надчерком обозначены установившиеся значения концентраций примесей первой группы. Концентрации примесей, относящихся к числу долгоживущих, вычисляется далее и использованием формулы (3.78).

Точность интегрирования зависит от ∆t′ и от констант химических реакций в (3.79). Для медленно реагирующих в воздушной среде примесей можно использовать достаточно большой шаг по времени, но он будет значительно меньше, если среди примесей будут быстро реагирующие (обычно ∆t′ = 0,1–5 мин, а ∆t = 5–10 мин).