
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания

МОДЕЛЬНАЯ ОЦЕНКА ЭКОЛОГИЧЕСКОЙ ОБСТАНОВКИ КОМПАНЕНТОВ ПРИРОДНОЙ СРЕДЫ С УЧЕТОМ АТМОСФЕРНЫХ ПРОЦЕССОВ
Айдосов А. , Айдосов Г. А., Заурбеков Н. С.,
4.1.1. Системы уравнений квазиоднородного приземного слоя
Слой вблизи поверхности земли (толщиной около 10–100 м) называется приземным слоем. Здесь, как правило, наблюдаются максимальные градиенты метеорологических элементов. Важной особенностью приземного слоя, в значительной мере оправдывающей выделение его в рамках планетарного пограничного слоя, является относительное постоянство по высоте турбулентных потоков. Хотя процессы в этом слое тесно связаны с процессами во всем пограничном слое, часто для решения ряда практических, важных задач достаточно установить внутренние связи между метеорологическими элементами и характеристиками турбулентности в одном только приземном слое [358–402].
Основой для физического описания приземного слоя атмосферы является теория подобия для турбулентного режима в стратифицированной среде [137]. В соответствии с этой теорией для приземного слоя атмосферы все статистические характеристики, пронормированные на масштабы длины 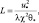 скорости
скорости 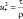 и температуры
и температуры 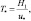 являются универсальными функциями безразмерной высоты
являются универсальными функциями безразмерной высоты 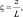 которая обычно принимается в качестве параметра гидростатистической устойчивости. Тогда вертикальные градиенты средних полей метеорологических элементов определяются с помощью некоторых функции φs(ς), φq(ς) зависящих от безразмерного аргумента ς. Таким образом, знание конкретного вида этих функций позволяет определить турбулентные потоки тепла, влаги и движения. Используя теорию подобия Монина-Обухова и эмпирические функции Бусинджера [137, 224] запишем систему уравнений приземного слоя:
которая обычно принимается в качестве параметра гидростатистической устойчивости. Тогда вертикальные градиенты средних полей метеорологических элементов определяются с помощью некоторых функции φs(ς), φq(ς) зависящих от безразмерного аргумента ς. Таким образом, знание конкретного вида этих функций позволяет определить турбулентные потоки тепла, влаги и движения. Используя теорию подобия Монина-Обухова и эмпирические функции Бусинджера [137, 224] запишем систему уравнений приземного слоя:
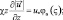
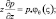 p = θ, q; (4.1)
p = θ, q; (4.1)
p – p0 = p*fθ(ςς0); ς = z/L; (4.2)
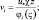
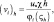 i = u, v; (4.3)
i = u, v; (4.3)
ςh = h/L; 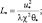
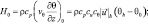 (4.4)
(4.4)
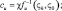
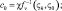
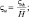
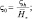
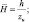
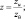 (4.5)
(4.5)
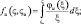
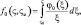 (4.6)
(4.6)
где 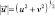 – модуль вектора скорости; u* – скорость трения; θ*, q* – масштабы потенциальной температуры и удельной влажности; h – высота приземного слоя; χ – постоянная Кармана; zu, zθ – параметры шероховатости для ветра и температуры (индексами 0 и h обозначены метеорологические поля при z = 0 и z = h соответственно); H0 – поток тепла; H0cu, cθ – коэффициенты трения и теплопередачи соответственно; H0φi, fi – непрерывные универсальные функции; H0θ0, q0 – температура и влажность подстилающей поверхности.
– модуль вектора скорости; u* – скорость трения; θ*, q* – масштабы потенциальной температуры и удельной влажности; h – высота приземного слоя; χ – постоянная Кармана; zu, zθ – параметры шероховатости для ветра и температуры (индексами 0 и h обозначены метеорологические поля при z = 0 и z = h соответственно); H0 – поток тепла; H0cu, cθ – коэффициенты трения и теплопередачи соответственно; H0φi, fi – непрерывные универсальные функции; H0θ0, q0 – температура и влажность подстилающей поверхности.
Комбинируя формулы (4.1)–(4.2) и принимая z = h, получим:
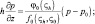 p = (θ, q);
p = (θ, q); 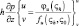 (4.7)
(4.7)
или
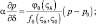 p = (θ, q);
p = (θ, q); 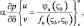 (4.8)
(4.8)
где 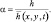
В дальнейшем формулы (4.8) будут служить краевыми условиями для задач локальных атмосферных процессов области выше приземного слоя, пока в предположении, что θ0, q0 известные функции от x, y, t.
При формулировке краевых условий (4.8) на нижней границе воздушной массы было сделано предположение, что температура и влажность подстилающей поверхности θ0, q0 заданы. Для прогностических задач это предположение довольно грубо, и поэтому для замыкания системы уравнений нужно сформулировать модель таким образом, чтобы температура и влажность подстилающей поверхности определялись наряду с другими метеоэлементами. Наиболее обоснованный в настоящее время подход к решению этой задачи состоит в формулировке совместной модели динамики пограничного слоя атмосферы во взаимодействии термически и орографический неоднородной подстилающей поверхностью. Для суши это модель температурного режима почвы с уравнением баланса тепла на границе с атмосферой и модель влагообмена.
Для простоты над водной поверхностью будем считать функции θ0, q0 заданными:
θ0 – f0(t); q = 0,622∙E0(θ0)/p, (4.9)
где E0 – упругость насыщения водяного пара при температуре θ0; p – атмосферное давление; f0(t) – температура поверхности воды.
Распределение температуры в почве описывается уравнением:
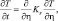 (4.10)
(4.10)
где 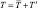 – абсолютная температура почвы; T′ – отклонения температуры почвы от среднесуточного значения,
– абсолютная температура почвы; T′ – отклонения температуры почвы от среднесуточного значения, 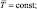 Ks(x, y, z) – коэффициент температуропроводности почвы предполагается заданным.
Ks(x, y, z) – коэффициент температуропроводности почвы предполагается заданным.
В качестве условии на поверхности Земли примем уравнение баланса тепла, которое имеет вид:
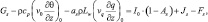 (4.11)
(4.11)
где 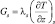 – теплопередача через поверхность почвы (индексом «0» отмечены величины, при z = 0); λs = csρsKs, ρs, cs, Ks – плотность, удельная теплоемкость, коэффициент температуропроводности почвы; ρ – плотность воздуха; I0 – приток суммарной коротковолновой солнечной радиации; As – альбедо подстилающей поверхности; Fs – эффективное длинноволновое излучение; as – безразмерный коэффициент, позволяющий учитывать тот факт, что в разных точках подстилающей поверхности, в следствие ее неоднородности, на испарения или конденсацию тратится неодинаковое количество тепла; Js(x, y, t) – функция, описывающая антропогенные источники тепла.
– теплопередача через поверхность почвы (индексом «0» отмечены величины, при z = 0); λs = csρsKs, ρs, cs, Ks – плотность, удельная теплоемкость, коэффициент температуропроводности почвы; ρ – плотность воздуха; I0 – приток суммарной коротковолновой солнечной радиации; As – альбедо подстилающей поверхности; Fs – эффективное длинноволновое излучение; as – безразмерный коэффициент, позволяющий учитывать тот факт, что в разных точках подстилающей поверхности, в следствие ее неоднородности, на испарения или конденсацию тратится неодинаковое количество тепла; Js(x, y, t) – функция, описывающая антропогенные источники тепла.
При штилевых температурах перепад температуры между уровнями z = 0 и z = zθ может достигать довольно больших значений. Поэтому, при решении (4.11) используется полуэмпирическая параметризационная формула для вязкого подслоя [37]:
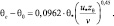 (4.12)
(4.12)
Уравнение (4.11) является краевым условием для (4.10) при z = 0. Второе граничное условие для (4.10) задается на глубине HП, где отсутствует суточное колебание температуры в почве, т.е.:
T = TП при z = –HП. (4.13)
Метод решения уравнения (4.10) с краевыми условиями (4.11), (4.13) рассмотрен в [27, 37]. Следуя [27, 37, 52], выпишем конечно-разностный аналог потока тепла в почву:
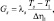 (4.14)
(4.14)
где Δη1 – шаг сетки по глубине; Δη1 T1 – значение температуры почвы на первом расчетном уровне.
Уравнение (4.10) решается численно, используя метод прогонки. Опуская промежуточные выкладки, представим решение в виде [27, 52]:
T1 = β1Ts + z1, (4.15)
где β1, z1 – прогоночные коэффициенты.
Подставляя (4.15) в (4.14), решение уравнения (4.11) представим в виде:
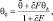 (4.16)
(4.16)
где 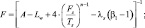
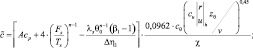
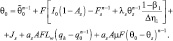
Таким образом, по вычисленному значению θ0, из (4.1,12) можно определить температуру θs. На практике для расчетов приземных характеристик используются следующие эмпирические формулы:
Формула Альбрехта [40]:
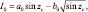 I0 ≥ 0; (4.17)
I0 ≥ 0; (4.17)
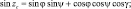 γ = (t – 12)π/12,
γ = (t – 12)π/12,
где zc – зенитный угол Солнца; φ – широта местности; γ – часовой угол Солнца; ψ – склонение Солнца; a0, b0 – заданные константы.
Формула Брендта [40]:
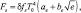 (4.18)
(4.18)
где δ – постоянная Стефана-Больцмана; fs – коэффициент серости почвы; ae, be – эмпирические константы; e – упругость водяного пара.
Формула Чарнока для определения параметра шероховатости над водой:
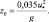 (4.19)
(4.19)
Формула Магнуса [40]:
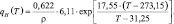 (4.20)
(4.20)
Надо отметить, что формула Альбрехта пригодна для расчета потока солнечной радиации для ровной местности. Известно, что температура приземного слоя воздуха и суммарное испарение увлажненной поверхности зависят от инсоляции деятельной поверхности. Следовательно, различие в инсоляции склонов, в зависимости от их экспозиции, могут привести в условиях орографической неоднородности подстилающей поверхности к значительным мезометрологическим контрастам. Поэтому для расчета потока солнечной радиации на поверхность склона используем формулу [18]:
Sh = S0cos α, (4.21)
где
cosα = sin zccos αr + cos ψα∙(sin φcos φcos γ – sin φcos ψαcos ψ)×
× sin αr + sin ψαcos ψsin γsin αr;
S0 – солнечная постоянная; αr – угол падения солнечных лучей на поверхность; ψα – азимут проекции нормали к склону на горизонтальную поверхность, отсчитываемый от плоскости меридиана (ψα считается положительным при отсчете с юга по часовой стрелке).
Функции αr, ψα вычислим следующим образом:
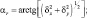
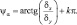 (4.22)
(4.22)
Значение параметра k меняется в зависимости от ориентации склона. По аналогии с (4.17) выпишем формулу для Sr – потока суммарной радиации на наклонную поверхность:
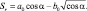 (4.23)
(4.23)
Нетрудно видеть, что при αr = 0 формулы (4.23) и (4.17) совпадают.