Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
МОДЕЛЬНАЯ ОЦЕНКА ЭКОЛОГИЧЕСКОЙ ОБСТАНОВКИ КОМПАНЕНТОВ ПРИРОДНОЙ СРЕДЫ С УЧЕТОМ АТМОСФЕРНЫХ ПРОЦЕССОВ
Айдосов А. , Айдосов Г. А., Заурбеков Н. С.,
4.3. Численные схемы блочной модели переноса вредных примесей в бароклинной атмосфере
Записав уравнения гидродинамики турбулентной атмосферы и диффузии примесей (4.39)–(4.50) для каждого блока модели с учетом взаимодействия между блоками и присоединив к ним уравнения переноса радиации, получим систему уравнений блочной модели локального климата:
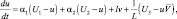(i = 1, 2, 3);
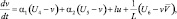(i = 1, 2, 3);
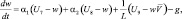(i = 1, 2, 3); (4.64)
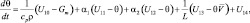(i = 1, 2, 3);
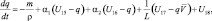(i = 1, 2, 3);
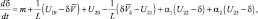(i = 1, 2, 3);
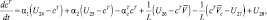(i = 1, 2, 3);
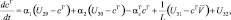(i = 1, 2, 3);
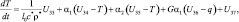(i = 0);
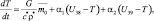(i = –1, –2);
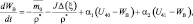(i = –1, –2);
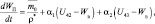(i = –1, –2);
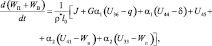(i = 0).
Скорость фазовых переходов влаги m в случае термодинамического процесса в воздухе, насыщенном водяным паром, определяется формулой:
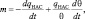
где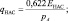 
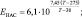
– скорость ветра; U1 = ui+1j; U2 = ui–1j; 
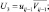U4 = vi+1j; U5 = vi–1j; 
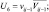U7 = wi+1j; U8 = wi–1j; 
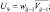U10 = επij; U11 = θi+1j; U12 = θi–1j; 
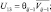U14 = Δθij; U15 = qi+1j; U16 = qi–1j; 
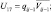U18 = Δqij; 
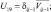U20 = Δδij; 
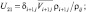U22 = δi+1j; U23 = δi–1j;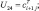 
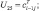
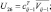
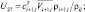
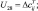
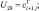
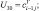
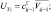
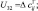U33 = επ0j; U34 = T1j; U35 = T–1j; U36 = q1j; U37 = ΔT0j; U38 = Ti+1j; U39 = Ti–1j; U40 = WB i+1j; U41 = WB i–1j; U42 = WП i+1j; U43 = WП i–1j; U44 = δ1j; U45 = ΔWB 0j,
где Δθij, Δqij, Δδij,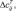 
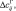ΔT0j, ΔWB 0j – антропогенные добавки в слои модели; i – номер блока по вертикали; j – номер блока по горизонтали; i – 1 – номер
соседнего блока снизу; i + 1 – номер соседнего блока сверху; j – 1 – номер блока, из которого дует ветер; j + 1 – номер следующего блока по воздушному потоку,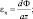 
Φ = J↓ – J↑ – U + G.
Следовательно, в предлагаемой блочной модели локального климата довольно просто с математической точки зрения записана основная система уравнений, но вследствие схематизации процессов появились дополнительные коэффициенты, при поиске которых максимально используются известные физические закономерности и выражающие теоретические, полуэмпирические и эмпирические формулы. От определения этих коэффициентов во многом будет зависеть степень приближения модели к действительности.
Определим коэффициенты двух блоков («Диффузия» и «Радиация») первого варианта модели. Расчетные модели для α1, α2 определяются непосредственно из системы уравнения:
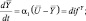
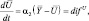
фиксируя время 
[7]:
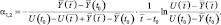
Для определения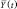 
привлечется непрерывная модель диффузии.
Параметры rk, ak, hk, pk, ek для чистой влажной атмосферы можно рассчитать с помощью следующих формул полученных [8]:
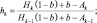
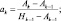
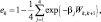
где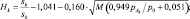 
Ak = 0,172(MWk∞)0,303;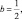 
где s0 – поток прямой радиации на верхней границе атмосферы (солнечная постоянная); sk – поток прямой радиации на уровне с давлением; pAk, p0 – давление у поверхности земли; M = f(h0) – число оптических масс атмосферы, где h0 – высота Солнца; Ak – функция поглощения прямой солнечной радиации водяным паром; Wk∞ – содержание водяного пара в столбе единичного сечения с основаниями k, ∞ (в г/см2):
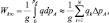
где ek – функция поглощения длинноволнового излучения водяным паром; Wk,h+1 – содержания водяного пара в столбе единичного сечения с основаниями k, k + 1; β1 = 0,166; β2 = 2,60; β3 = 36,2; β4 = 114.
Моделировался суточный ход температуры в одной ячейке модели в летний, безоблачный, безветренный день для широты 55,7° и склонения Солнца 23,4°. Поверхность считалась достаточно увлажненной (q0 = qНАС(T0) с коэффициентом отражения (альбедо) r = 0,2. Твердые и газообразные примеси не учитывались. Задавалось начальное состояние: T–1 = 287; T0 = 283; θ1 = 285; θ2 = 282; θ3 = 260; q1 = 0,0054; q2 = 0,0042; q3 = 0,0014.
Система уравнений (4.64) интегрировалась методом Рунге-Кутта с шагом по времени t = 1 ч. Результаты расчетов сравнивались с данными экспедиционных наблюдений.