
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания

МОДЕЛЬНАЯ ОЦЕНКА ЭКОЛОГИЧЕСКОЙ ОБСТАНОВКИ КОМПАНЕНТОВ ПРИРОДНОЙ СРЕДЫ С УЧЕТОМ АТМОСФЕРНЫХ ПРОЦЕССОВ
Айдосов А. , Айдосов Г. А., Заурбеков Н. С.,
5.3. Процессы, определяющие перенос загрязняющих веществ в атмосфере при аварийных выбросах
Распределение температуры в основном ответственно за степень перемешивания выброшенных веществ и высоты, до которой наблюдается перемешивание. В настоящее время большинство исследователей определяют верхнюю границу слоя перемешивания (высоту пограничного слоя атмосферы) по наличию задерживающих слоев инверсии (или изотермии). Однако известно, что загрязняющие вещества могут проникать через инверсионные слои и поэтому высоту слоя перемешивания следует либо определять по затуханию турбулентных потоков, либо задавать так, чтобы загрязняющие вещества заведомо не проникали за расчетную область. Измерения вертикальных профилей различных загрязняющих веществ показывают, что большинство из них сосредоточено в нижнем двухкилометровом слое атмосферы. В этой связи в модели в качестве верхней границы была выбрана высота 5 км, на которой никогда не наблюдалось значительных концентраций загрязняющих веществ, выброшенных наземными или приподнятыми источниками [413, 414, 416].
Степень перемешивания, которая зависит от устойчивости атмосферы параметризовалась через введение переменного по высоте профиля коэффициента турбулентной диффузии.
Вертикальный коэффициент турбулентности вычислялся по алгоритму, подробно изложенному во втором разделе.
Весь рассматриваемый слой атмосферы (до 5 км) был разделен на две области: приземной подслой и слой перемешивания.
В приземном подслое (до 100 м) коэффициент турбулентности оценивался по методу с выделением двух режимов турбулентности: устойчивой и неустойчивой стратификации, которая определялась по безразмерной высоте ξ:
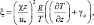 (5.1)
(5.1)
где χ – постоянная Кармана, равная 0,4; u* – скорость динамического трения; γa – влажноадиабатический градиент температуры.
Выше приземного слоя, коэффициент турбулентности вычислялся по методу Блокадара. Его величина складывается из двух слагаемых: турбулентности на верхней границе приземного слоя (Kz(h)) и турбулентности Ke, определяемой стратификацией выше приземного слоя в зависимости от степени конвективной неустойчивости:
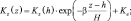 (5.2)
(5.2)
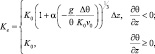
где h – высота приземного подслоя; θ – потенциальная температура; K0, v0 – фоновые значения вихревой диффузии и вязкости, равные соответственно 0,3 и 0,63; α, β – эмпирические константы, равные соответственно 0,3 и 1,0.
При описании процессов адвективного переноса и турбулентного рассеяния выброса АС в атмосфере необходимо учитывать, что выбрасываемая газоаэрозольная смесь имеет определенную скорость, связанную как с ее начальной кинетической энергией, так и с действующими на нее силами плавучести, обусловленными разностью температур смеси и окружающего воздуха. Таким образом, в реальных условиях существует как бы эффективная высота трубы, которая больше ее реальной высоты на Δh. Известны различные подходы к определению Δh, в модели выбрано соотношение рекомендованное Главной Геофизической Обсерваторией (Россия):
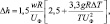 (5.3)
(5.3)
где w, ΔT – скорость и перегрев газо-аэрозольного выброса; UΦ, T – скорость ветра и температура окружающего воздуха; R – радиус устья трубы.
Для полного описания распространения газо-аэрозольного выброса АС в атмосфере, необходимо учесть процессы вымывания, влажного выведения, радиоактивного распада и трансформации химических и агрегатных состояний радионуклидов. Для учета всех этих процессов вводят поправки в виде экспоненциальных множителей с соответствующими постоянными λi (i = 1, S), которые выбираются эмпирически для каждого процесса и зависят от конкретных химических составов выброса и погодных условий.
Согласно первому подразделу третьего раздела, распространение загрязняющих веществ в атмосфере описывается трехмерным уравнением сохранения массы:
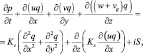 (5.4)
(5.4)
где q – объемная концентрация примеси; u, v, w – компоненты скорости ветра, переменные в пространстве и времени; vg – скорость гравитационного оседания; Ks, Kz – коэффициенты горизонтальной и вертикальной диффузии; IS – поле источников (мгновенных или непрерывных) выбросов, являющиеся функцией пространства и времени.
Горизонтальные компоненты скорости ветра u, v – являлись входными параметрами модели и определялись из объективного анализа.
Вертикальный компонент скорости ветра w определялся из уравнения неразрывности:
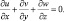 (5.5)
(5.5)
Скорость гравитационного оседания описывалась законом Стокса и для частиц с радиусом r ≤ 10 мкм определялась:
vg = 1,26∙10–5∙ρ∙r2, (5.6)
где ρ – плотность загрязняющих веществ; r – радиус частиц.
Уравнение (5.4) решалось при следующих начальных и граничных условиях:
q(x, y, z, 0) = qΦ(x, y, z), (5.7)
где qΦ(x, y, z) – фоновое значение объемной концентрации примеси для первых суток расчета:
q(x, y, z, 0) = q0(x, y, z), (5.8)
где q0(x, y, z) – объемная концентрация примеси, сформировавшаяся за предшествующие сутки.
На верхней границы области (Н = 5 км) задаются нулевая концентрация:
q(x, y, z, H) = 0 (5.9)
На нижней границе (подстилающая поверхность) задаются условия полного поглощения на предшествующем шаге во времени и рассчитываются полный (турбулентный и адвективный) поток примеси на подстилающую поверхность на расчетном шаге по времени:
q(x, y, 0, t – Δt) = 0; (5.10)
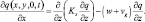
Также рассматривается постановка граничных условий третьего рода:
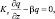 (5.11)
(5.11)
где β – эмпирический констант, определяющий поглощение примеси подстилающей поверхности.
Условие (10) для тяжелых примесей с большей скоростью гравитационного оседания, для легких примесей условие (11). Кроме того, оно учитывает турбулентный подъем примеси, что позволяет рассматривать подстилающую поверхность как поле вторичных источников и рассчитывать вторичный перенос загрязнителя.
При задании граничных условий на боковых границах обычно пользуются условиями типа Дирихле (задано значение функции), или условиями типа Неймана (задан градиент функции по нормали к границе), или задается свободная граница:
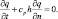 (5.12)
(5.12)
Последнее условие кажется наиболее физичным, но из-за не совсем строгого определения фазовой скорости (cph) было решено заменить ее реальной скоростью, причем для лучшего согласования значений функции на границе и внутри расчетной области, кроме оператора нормального к границе добавлялись операторы с касательными компонентами скорости. Таким образом, боковые граничные условия имели следующий вид:
– в области втока:
q = 0;
– в области вытекания:
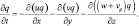 (5.13)
(5.13)
Постановка боковых граничных условий и их конечно-разностная аппроксимация подробно исследованы в работе [22] и сделан вывод, что граничные условия [22] в области вытекания позволяют полностью избежать отражения на границе расчетной области.
Распространение примеси в условиях сложного рельефа и над ровной поверхностью будут существенно различаться из-за деформации потока препятствиями. При наличии рельефа система (5.4)–(5.13) должна решаться в области с криволинейной границей. Конкретная форма области, при условии жесткой горизонтальной стенки на высоте Н будет определяться функцией, описывающей форму
рельефа ZS(x, y). Чтобы избежать трудностей, связанных с численными интегрированиями в криволинейной области, обычно переходят к новым координатам, в которых расчетная область становится прямолинейной. Было выбрано преобразование, детально описанное во втором разделе, удовлетворяющее следующим условиям: преобразование обратимо; идентично при ZS = 0 и ZS = Н; имеет непрерывные вторые производные; сохраняет ошибку аппроксимации того же порядка, что и в декартовой системе координат, что достигается близостью к 1 его определителя.
Преобразование имеет вид:


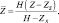 (5.14)
(5.14)
Уравнение неразрывности в новых координатах имеет вид:
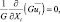 (5.15)
(5.15)
где  (i = 1, 2, 3) – новые компоненты скорости ветра; G = (H – ZS)/H – якобиан преобразования.
(i = 1, 2, 3) – новые компоненты скорости ветра; G = (H – ZS)/H – якобиан преобразования.
Новые компоненты скорости определяются матрицей перехода:
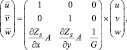 (5.16)
(5.16)
где 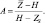
Трехмерное уравнение сохранения массы в новой системе координат имеет вид:
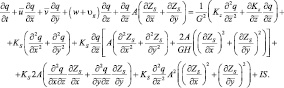 (5.17)
(5.17)
Граничные и начальные условия для решения этого уравнения выбираются такие же, как и для модели над однородной поверхностью.
В модели рассчитываются конвективные движения, вызванные неравномерностью нагрева подстилающей поверхности (температура водоема-охладителя) и неравномерностью температуры в приземном слое (остров тепла над водоемом-охладителем):
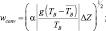
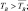
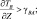
wconv = 0; 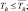
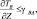 (5.18)
(5.18)
где α – эмпирическая константа; TB – виртуальная температура; 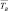 – средняя по площади виртуальная температура; γBA – влажно-адиабатический градиент температуры; ΔZ – толщина слоя.
– средняя по площади виртуальная температура; γBA – влажно-адиабатический градиент температуры; ΔZ – толщина слоя.
Таким образом, вертикальные движения, участвующие в рассеянии газоаэрозольных выбросов складываются из крупномасштабных вертикальных движений, рассчитываемых из уравнения неразрывности с учетом орографии и конвективных вертикальных движений:
w = wmacr + wconv. (5.19)
В предлагаемой модели для численного решения системы уравнений (5.4)–(5.13) был выбран конечно-разностный метод, хорошо зарекомендовавший себя во многих численных моделях переноса примеси. При этом дифференциальные уравнения, описывающие исходную задачу аппроксимировались конечно-разностной схемой:
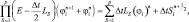 (5.20)
(5.20)
где 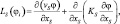 (S = 1, 2, 3), Si – члены уравнения, описывающие источники; Δt – шаг по времени.
(S = 1, 2, 3), Si – члены уравнения, описывающие источники; Δt – шаг по времени.
Схема (5.20) является двухслойной разностной схемой с расщепляющимся оператором, имеет второй порядок точности по времени и является абсолютно устойчивой.
При реализации разностной схемы (5.20) решение находилось не для самой функции φ на g + 1 шаге, а для ее превращения за шаг по времени 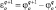 Этот метод реализации позволил избавиться от аппроксимации смешанных производных. Реализация схемы по каждому пространственному направлению осуществлялась методом прогонки.
Этот метод реализации позволил избавиться от аппроксимации смешанных производных. Реализация схемы по каждому пространственному направлению осуществлялась методом прогонки.
Основной трудностью, с которой приходится сталкиваться при формулировке разностной задачи, является аппроксимация адвективных операторов уравнения переноса. Сложность заключается в том, что при решении уравнения для положительно определенных функций конечно-разностная схема должна удовлетворять следующим основным требованиям:
– обладать малой счетной вязкостью, то есть иметь порядок аппроксимации по времени и пространству не ниже второго;
– быть монотонной, то есть не генерировать нефизических, отрицательных значений;
– быть консервативной, то есть удовлетворять уравнению сохранения массы в заданном объеме;
– иметь малую фазовую ошибку, то есть переносить максимальные значения функции, и ее градиенты с заданной скоростью.
В этой связи во втором разделе был проведен анализ известных в литературе и наиболее часто используемых в гидродинамических моделях конечноразностных схем для численного решения уравнения адвекции.
В этой же части работы приведен способ построения гибридной саморегулирующейся схемы, основанной на схемах направленных и центральных разностей, отвечающей перечисленным требованиям. Гибридный оператор L″(φi), аппроксимирующий адвективную часть дифференциального пространственного оператора имеет вид:
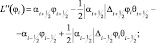 (5.21)
(5.21)
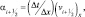 S = 1, 2, 3;
S = 1, 2, 3;
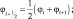
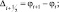
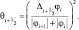
Этот гибридный оператор аппроксимирует дифференциальный оператор со вторым порядком точности, сохраняя при этом локальную монотонность и на не гладких участках решения (при θ → 1) сводится к схеме направленных, а на гладких (при θ → 0) – к схеме центральных разностей.
Диффузионная часть дифференциального оператора 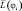 аппроксимировалась со вторым порядком точности по трехточечной схеме:
аппроксимировалась со вторым порядком точности по трехточечной схеме:
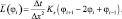 (5.22)
(5.22)
В случае введения неравномерного шага и переменного по вертикали коэффициента вертикальной диффузии дифференциальный оператор L3(φi) аппроксимировался модифицированными операторами:
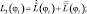
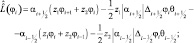
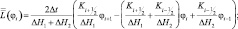
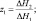
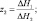 ΔH1 = Hi+1 – Hi; ΔH1 = Hi – Hi–1.
ΔH1 = Hi+1 – Hi; ΔH1 = Hi – Hi–1.
Программа реализована на персональной ЭВМ PENTIUM, на языке программирования ФОРТРАН-77.
Функциональная блок-схема программы
Основная программа MAIN является управляющей и осуществляет ввод массивов и констант, необходимых для работы программы, таких как количество точек сетки по горизонтали и вертикали.
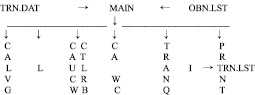
Далее в диалоговом режиме с экрана дисплея вводится информация о количестве суток на которое ведется расчет, о количестве, местоположении, высоте и мощности источников как непрерывного действия, так и дающих аномальный выброс на заданном шаге по времени.
Из файла данных TRN.DAT считывается информация о высоте уровней на которых ведется расчет и массивы, определяющие геометрические высоты и параметр шероховатости в точках регулярной сетки.
Из файла данных OBN.LST считывается информация о вертикальном профиле давления, трехмерных полях температуры, точки росы и компонентов скорости ветра в узлах регулярной сетки, полученные в результате объективного анализа этих метеоэлементов. Программа осуществляет обращение ко всем параметрическим процедурам, а также интегрирование по времени на заданное число суток.
Процедура CALVG осуществляет расчет дополнительной исходной информации: скорости гравитационного оседания в зависимости от радиуса; плотности вещества и атмосферного давления; пересчет временного шага, исходя из выполнения условия Куранта-Фридрихса-Леви.
Процедура CALCW осуществляет расчет фоновых вертикальных движений путем интегрирования уравнения неразрывности.
Процедура CTURB осуществляет расчет вертикальных профилей коэффициента турбулентного обмена в зависимости от устойчивости атмосферы, параметров шероховатости подстилающей поверхности и скорости ветра.
Процедура CALWC осуществляет расчет конвективных вертикальных движений, связанных с неравномерным перегревом подстилающей поверхности и в частности с температурным влиянием прудов охладителей.
Основным модулем является процедура TRANQ, которая осуществляет численное интегрирование уравнения модели в пространственно – временных координатах. Она определяет изменения массовой концентрации загрязняющих веществ и оценку их суточного осаждения на подстилающую поверхность в зависимости от направления и скорости ветра, скорости гравитационного оседания частиц, а также величины коэффициентов турбулентной диффузии.
Процедура PRINT выводит на экран дисплея и АЦПУ поля плотности осажденных веществ (г/м2), сумму выброшенных загрязняющих веществ, оставшуюся в атмосфере суммарную концентрацию и суммарную массу осажденных веществ.
Процедура также выводит на экран дисплея и АЦПУ карты изолиний, плотности осажденных загрязняющих веществ и приземных концентраций.
Как уже упоминалось выше, результаты проверки численной схемы, используемой для аппроксимации дифференциального уравнения переноса примеси и граничных условий для этого уравнения подробно изложены во втором разделе. В этом разделе мы опишем тестовые эксперименты, которые были проведены для доказательства правильности работы модели.
Из файла данных синоптических и аэрологических наблюдений выбирались и затем интерполировались в узлы заданной сетки давление, температура, точка росы и компоненты скорости ветра (U, V). Область счета составляла 30×30 км, с шагом сетки Δх = Δy = 1 км по горизонтали и 5 км с переменным по высоте шагом по вертикали. Затем из уравнения неразрывности рассчитывался вертикальный компонент скорости W. Задавалось пять непрерывных источника, выбрасывающих загрязняющие вещества. Координаты источников соответствовали следующим точкам сетки:
– первый источник: i = 4, j = 4, k = 3;
– второй источник: i = 8, j = 4, k = 2;
– третий источник: i = 6, j = 16, k = 2;
– четвертый источник: i = 16, j = 6, k = 2;
– пятый источник: i = 10, j = 10, k = 3.
Количество выбрасываемой примеси 0,5; 1,0; 1,0; 0,5; 1,0 г/с соответственно. Эффективная высота выбросов составляла 100 м, что соответствовало третьему уровню модели (k = 3).
На шестидесятом шаге по времени (через 6 часов) на пятом источнике происходил аномальный выброс, когда за один шаг по времени (360 с) выбрасывалось 104 г загрязняющих веществ. Эффективная высота аномального выброса составила 190 м, что соответствовало четвертому уровню модели (k = 4). Далее под действием поля ветра, горизонтальной и вертикальной диффузии происходило распространение загрязняющих веществ и их выпадение на подстилающую поверхность в основном за счет их гравитационного и турбулентного оседания.
Через каждые сутки на печать выдавались поля:
– выпавшей на подстилающую поверхность примеси (г);
– оставшейся в воздухе примеси (г) на 40, 100, 190, 350 м соответственно.
Поле выпавшей примеси выдавалось также в виде изолиний для наглядности и удобства анализа. Также для контроля выдавались значения: суммы выброшенных загрязняющих веществ (г); суммы выпавшей на подстилающую поверхность примеси (г); суммы оставшихся в атмосфере веществ (г) и отношение выпавших к выброшенным источниками загрязняющих веществ в процентах. На рис. 24 приведены изолинии плотности (в мкг/м2∙сутки) выпадения аэрозольной примеси с плотностью ρ = 1 г/см3 и радиусом 1МКМ от пяти описанных выше источников, через 1 сутки.
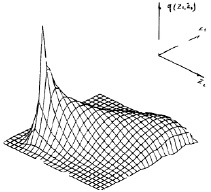
а
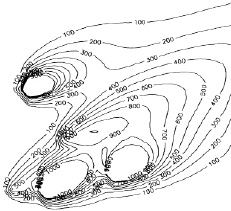
б
Рис. 24
а – распределение примесей от одного источника;
б – изолинии плотности выпадения (в мкг м2сут)
Результаты численных экспериментов на ЭВМ с моделью переноса загрязняющих веществ по реальным данным дают возможность говорить о достаточно реалистических прогнозах как траекторий переноса примеси в заданных регионах, так и о значениях концентраций примесей в атмосфере. Программная реализация модели и организация начальных данных позволяют легко модифицировать параметры настройки модели, выбирать произвольный регион на территории Северного полушария, число точек сетки интегрирования, количество уровней, координаты источников выбросов и т.д.
Разработанные программные средства могут быть использованы для численных прогностических экспериментов при моделировании переноса примесей в атмосфере от поля источников с различной интенсивностью и плотностью загрязняющих веществ.