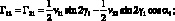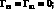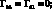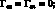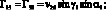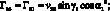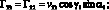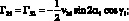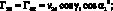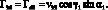Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
ДИНАМИЧЕСКОЕ ПОВЕДЕНИЕ ОБОЛОЧКИ ИЗ КОМПОЗИЦИОННЫХ МАТЕРИАЛОВ тетрагональнОЙ СТРУКТУРЫ
Немеребаев М. Н., Бекмуратов М. М., Орынбаев С. А., Актаев Е. К.,
3.2. Функции динамической податливости изолированного стержня
Вынужденные колебания стержня постоянного сечения, в пределах справедливости гипотезы плоских сечений, под действием единичной гармонической силы, приложенной в произвольной точке S по оси x, опиливаются, как известно, следующими уравнениями [9, 151]:
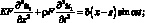
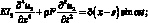
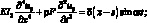(3.9)
|
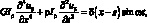
где E – |
модуль упругости; |
|
G – |
модуль сдвига; |
|
ρ – |
массовая плотность материала; |
|
F – |
площадь поперечного сечения стержня; |
|
I2, I3 – |
моменты инерции сечений стержня относительно оси 2 и 3 соответственно; |
|
Iρ – |
полярный момет инерции; |
|
u1, u2, u3 – |
перемемещения в направлении оси 1,2 и 3; |
|
u4 – |
угол закручивания относительно оси 1; |
|
δ(x – s) – |
разрывная функция Дирака 1-го рода. |
Запишем граничные условия в виде
u1 = 0;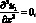 
u2 = 0; 
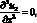u3 = 0; (3.10)
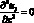, u4 = 0 при x = 0, x = l.
Будем искать решение (3.9) в виде
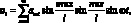(3.11)
где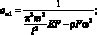 
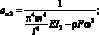
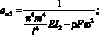(3.12)
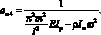
Основными элементами матрицы функции динамической податливости стержней будут амплитудные значения полученных перемещений, т.е.
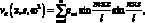i = 1, 2, 3, …, k. (3.13)
Отличными от нули являются также элементами v55, v66, v35, v53, v62, v26. Они определяются через основные, дифференциальными операциями.
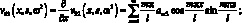
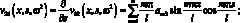
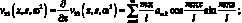(3.14)
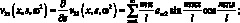
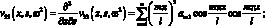
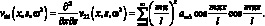
В целом матрица функции динамической податливости прямого незакрученного стержня постоянного сечения имеет вид.
(3.15)
Функции динамической податливости стержней по направлениям осей 1, 2 и 3 совпадающих с осью каркаса, его радиусом и осью, расположенной в нормальном сечении под прямым углом к радиусу, обозначен через Гij (x, s, w2), где для простоты в индексах опущены штрихи.
Элементы матрицы Гij выражаются через vij следующим образом:
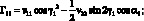
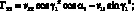
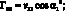
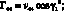
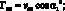(3.16)
