Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

ДИНАМИЧЕСКОЕ ПОВЕДЕНИЕ ОБОЛОЧКИ ИЗ КОМПОЗИЦИОННЫХ МАТЕРИАЛОВ тетрагональнОЙ СТРУКТУРЫ

Немеребаев М. Н., Бекмуратов М. М., Орынбаев С. А., Актаев Е. К.,

3.4.6. Построение функции динамической податливости от единичного изгибающего момента (P6)

Аналогично п. 3.4.5 получаем:

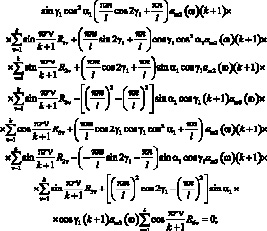(3.62)

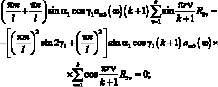
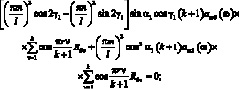
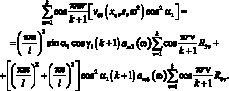
Частотные уравнение в этом случае имеет вид:

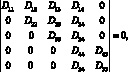(3.63)

где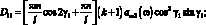

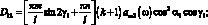
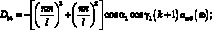
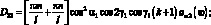
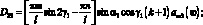
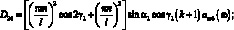
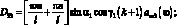(3.64)

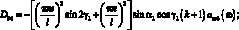
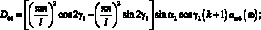
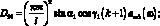
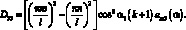
Вычисление бесконечного числового ряда

Рассмотрим бесконечный числовой ряд из выражения: (3.45)

Для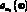

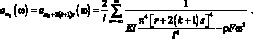(3.65)

Бесконечный числовой ряд в этом выражении может быть просуммирован при помощи теории вычетов [79].

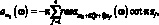(3.66)

здесь zf – полюса; 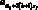или корни уравнения.

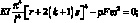(3.67)

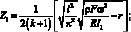
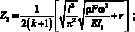(3.68)

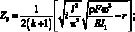
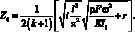
Замечаем, что корни zf имеют первую кратность, а следовательно, являются полюсами І порядка для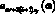

В этом случае имеем:

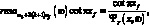(3.69)

где

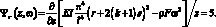
Подставив в (3.66) выражение для вычетов (3.69) и значении корней (3.68) после неложных преобразований получим:

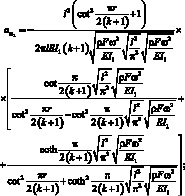(3.70)

для бесконечного числового ряда

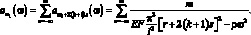(3.71)

По теории вычетов

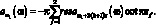(3.72)

Корни уравнения

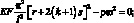
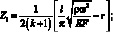
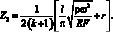(3.73)

Поставляя в (3.72) выражение для вычетов (3.69) и значеиня корней (3.73), после преобразований получим:

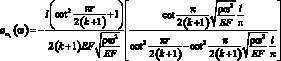(3.74)

Аналогично для 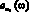получим:

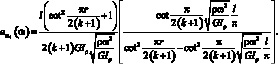(3.75)