Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

ДИНАМИЧЕСКОЕ ПОВЕДЕНИЕ ОБОЛОЧКИ ИЗ КОМПОЗИЦИОННЫХ МАТЕРИАЛОВ тетрагональнОЙ СТРУКТУРЫ

Немеребаев М. Н., Бекмуратов М. М., Орынбаев С. А., Актаев Е. К.,

4.1. Вывод исходных системы уравнений

Рассмотрим конструкцию, выполненную в виде сетчатой оболочки из композиционного материала. Ребра, образующие сетчатую оболочку, представляют собой однонаправленный композиционный материал, состоящий из большого числа, волокон, соединенных связующим. Однонаправленный композитный материал характеризуется модулем упругости Е и модулем сдвига G. Ребра прямоугольного сечения характеризуется толщиной δ и высотой h (рис. 4.1).

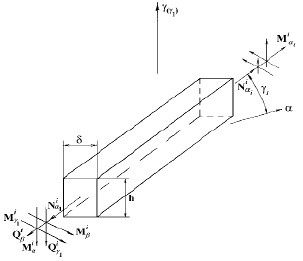
Рис. 4.1

Срединную поверхность оболочки отнесем к системе координат α, β, γ причем оси α и β являются криволинейными координатами, а ось γ направлена по нормами к этой поверхности.

Будем считать, что ребра сетчатой конструкции располагаются под углом φ к оси λ. При этом угол φ может принимать различные значения от 0 до 90°.

Выделим элемент і-го ребра, наклоненного к оси λ под углом φі и отнесем его к декартовой системе координат α, β, γ.

Оси β и γ являются главными центральными осями инерции поперечного сечения ребра. В ребре действует шесть внутренних силовых факторов: осевые усилия 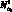, перерезывающие усилия 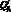и , и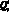згибающие моменты в плоскости 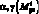, в плоскости 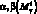и крутящие моменты .

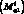Перейдем от системы координат α1, β1, γ к системе координат α, β, γ, провернутой относительной оси α на угол φі. Заменим рассматриваемую оболочку условно однородной. При этом будем считать, его усилия и момент распределены по сечению непрерывно. Следовательно, для погонных усилий и моментов, возникающих в продольных сечениях оболочки, в координатах α, β, γ получим следующие соотношения [29]:

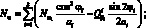
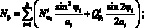
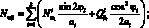(4.1)

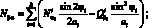
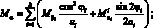
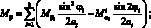
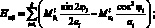
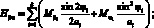
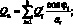
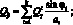
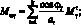
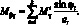
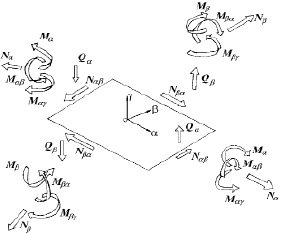
Рис. 4.2

При положительном направлении сил и моментов, действующих в оболочке (как показана на рис. 4.2), уравнения равновесия для выделенного элемента оболочки в системе координат α, β, γ запишутся в следующей форме [17]:

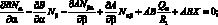
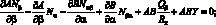
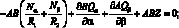
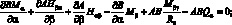(4.2)

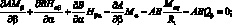
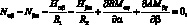
где A и B –	коэффициенты первой квадратичной формы серединной поверхности;
R1, R2 –	главные радиусы кривизны.

Принятая система уравнений равновесия (4.2) отличается от классической наличием моментов Mαγ и Mβγ, действующих в плоскостях касательных к срединной поверхности оболочки и представляет собой вариант теории оболочек, соответствующий моментной теории [112].

Зависимость усилий и моментов от деформации определяется смешанным вариационным методом [121].

Энергия деформации, приходящейся на единицу площади срединной поверхности через усилия и моменты в ребрах имеет вид:

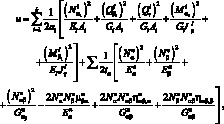(4.3)

Здесь Fi и   –	площадь и моменты инерции относительно осей;
–	полярный момент инерции поперечного сечения i-го ребра сетчатой оболочки;
Ei, Gi –	модули упругости однонаправленного композитного материала.

Теперь, согласно [121] можно получить соотношения между внутренними усилиями и моментами, действующими в ребрах оболочки, с одной стороны и средними перемещениями u, v,w, а также средними углами поворота Ψα, Ψβ, Ψαβ с другой. Для этого следует минимизировать выражение для энергии деформации (4.3) с учетом уравнений равновесия (4.2) и статических соотношений (4.1)

Рассматривая ктнематические переменные u, J, w, Ψa, Ψb, Ψαb, εa, εb, γαb, γβa, χa, χb, χαb, θa, θb, ωa, как множители Лагранжа, запишем функционал в виде:

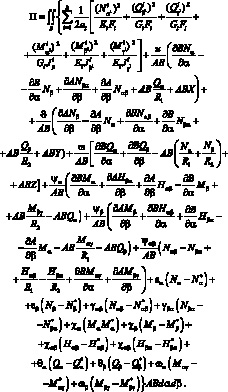(4.4)

Здесь величины, обозначенные штрихами [*], соответствуют правым частям статических соотношений (4.1).

Таким образом, может быть поставлена задача о минимизации функционала (4.4), имеющего следующий вид:

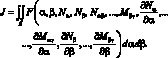(4.5)

Условием экстремума функционала (4.5) является равенство нулю его первой вариации:

δJ = 0 (4.6)

исходя из этого, запишем систему уравнений Остроградского:

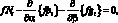(4.7)

где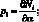

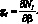
Граничные условия:

uδNα = 0; ϑδNβ = 0; uδNβα = 0. (4.8)

Раскрывая (4.7), получим соотношения упругости, связывающие усилия и моменты в ребрах со множителями Лагранжа:

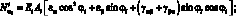
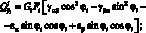
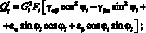(4.9)

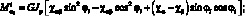
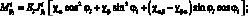
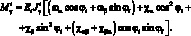
Рассматриваемая конструкция из композиционного материала является симметричной структурой, для которой первая квадратная форма срединной поверхности является постоянной. В этом случае геометрические соотношения множителей Лангранжа преобразуется в следующие выражения:

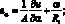
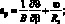
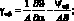
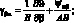
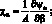
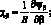(4.10)

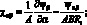
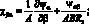
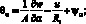
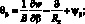
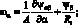
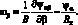
Из (4.4) и (4.10) следует, что множители Ланрганжа u,v,w представляют собой перемещения срединой поверхности оболочки по осям координат α, β, Ψα, Ψβ, Ψαβ, Ψβα – углы поворота относительно оси β, α и γ; εα, εβ, γαβ, γβα – относительные линейные и сдвиговые деформации срединной поверхности; ϰα, ϰβ, ϰαβ, ϰβα – изменения кривизны; θα и θβ – деформация поперечного сдвига; ωα, ωβ – углы поворота элемента оболочки относительно оси γ.

Поставляя выражения (4.9) в (4.1), получим уравнения для усилий и моментов в сетчатой оболочке через некоторые обобщенны жесткости ребра и соответствующие деформации:

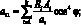
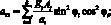
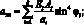
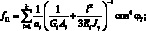
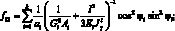
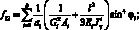
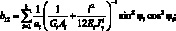
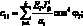
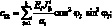
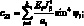
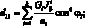
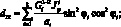(4.11)

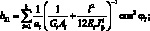
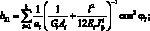
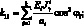
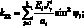
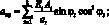
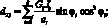
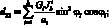
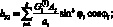
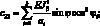
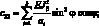
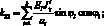
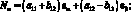
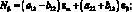
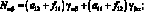
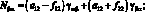
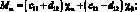
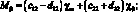
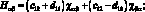
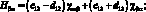
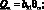
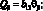
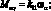
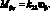
Система уравнений равновесия в усилиях также упрощается и имеет вид:

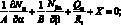
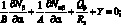
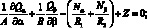(4.12)

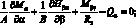
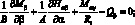
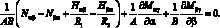
Подставляя выражения [4.12], получаем систему дифференциальных уравнений равновесия в перемещениях:

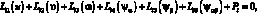(4.13)

i = 1, 2, 3, ..., 6.

Здесь для линейных дифференциальных операторов Lіj имеем:

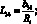
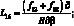
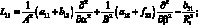
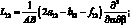
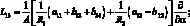
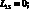
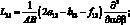
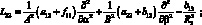
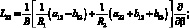
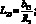
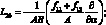
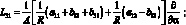
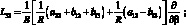
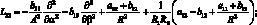
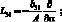
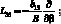
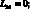
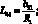
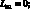
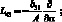
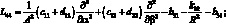(4.14)

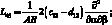
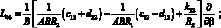
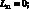
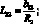
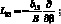
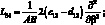
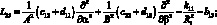
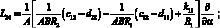
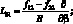
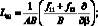
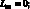
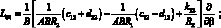
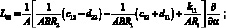
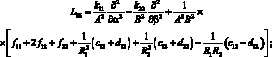
P1 = X; P2 = Y; P3 = –Z.

Полученная система уравнений (4.13) в общем случае не обладает симметрией. Однако в некоторых частных случаях, например, для рассматриваемой сетчатой оболочки, она становится симметричной относительно главной диагонали.

В результате решения системы из шести дифференциальных уравнений (4.13) могут быть определены шесть неизвестных: три перемещения u(αβ), v(αβ), w(αβ) и три угла поворота Ψα, Ψβ, Ψαβ.

С помощью полученных величин с учетом соотношений (4.9) и (4.11) могут быть определены усилия и моменты в ребрах. По найденным усилиям и моментам определяются напряжения в отдельных частях рассматриваемой конструкции, которые затем сравниваются с допускаемыми. Это дает возможность судить о работоспособности каждого элемента конструкции.
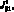