Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

ДИНАМИЧЕСКОЕ ПОВЕДЕНИЕ ОБОЛОЧКИ ИЗ КОМПОЗИЦИОННЫХ МАТЕРИАЛОВ тетрагональнОЙ СТРУКТУРЫ

Немеребаев М. Н., Бекмуратов М. М., Орынбаев С. А., Актаев Е. К.,

4.2. Колебания цилиндрической сетчатой оболочки из композиционного материала

Рассмотрим конструкции, выполненную в виде круговой цилиндрической сетчатой оболочки. Несущаю часть рассматриваемой конструкции представляет собой сетчатую структуру из композиционного материала, выполненную в виде спиральных ребер, соединенных между собой на опорных шпангоутах. Срединная поверхность ее отнесена к системе координат α, β, γ. Спиральные ребра расположены под углом ±φ к оси αλ (см. рис. 4.3).

Дифференциальные уравнения равновесия в перемещениях для рассматриваемой сетчатой цилиндрической оболочки могут быть получены на основе соотношений (4.2).

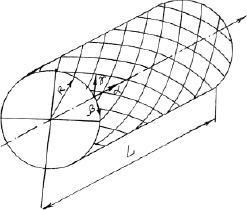
Рис. 4.3

В выбранной системе координат α, β, γ коэффициенты А и В, главные радиусы кривизны R1 и R2 координатной поверхности цилиндрической оболочки определяются [5]:

A = B = 1; 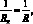(4.15)

где R – радиус оболочки.

В этом случае уравнения равновесия в усилиях можно записать в следующей форме [112]:

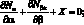
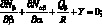
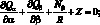(4.16)

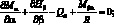
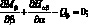
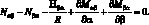
Геометрические соотношения, связывающие компоненты деформации (4.10), будут иметь вид:

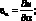
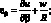
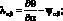
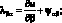(4.17)

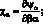
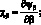
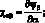
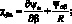
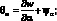
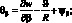
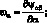
Соотношения для усилий и моментов, действующих в рассматриваемой оболочке выражаются:

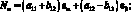
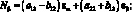
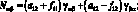
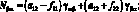(4.18)

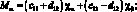
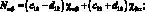
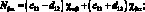
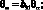
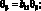
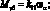
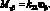
В выражениях (4.18) введены обобщенные жесткости сетчатой оболочки aij, cij, bij, dij, fij, kij зависящие от угла φ, от расстояния между осями ребер одного семейства аі и соответствующих жесткостей ребер при растяжении и сжатии (Fі Fс), жесткостей при сдвиге тангенциальной и нормальной плоскостях ребра GFci, жескостей при изгибе в этих же плоскостях (ЕJyi, EJzc) и жескости при кручении (GJρc)

A = πr2.

Обобщенные жескости сетчатой оболочки, входящие в выражения (4.18) имеют вид:

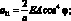
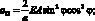
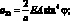
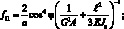
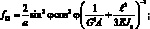(4.19)

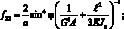
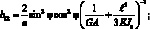
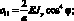
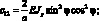
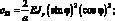
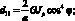
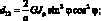
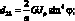
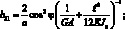
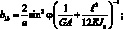
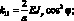
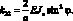
Тогда системы дифференциальных уравнений равновесия, рассматриваемой цилиндрической сетчатой оболочки в перемещениях имеет вид:

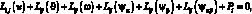(4.20)

где i = 1, 2, 3, ..., 6; j = 1, 2, 3, ..., 6.

где для линейных дифференциальных операторов Lij имеем:

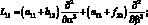
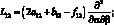
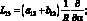
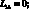
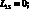
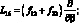
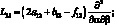
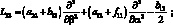
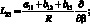
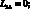
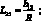
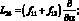
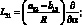
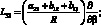
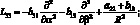
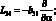
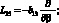
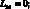
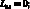
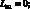
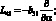
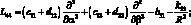(4.21)

;

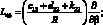
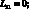
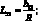
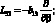
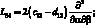
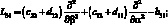
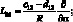
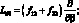
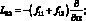
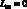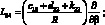
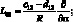
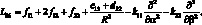
Как известно, уравнения движения, описывающие колебания оболочки, могут быть получены из уравнений равновесия, путем замены грузовых членов Х, Y, Z соответствующими инерционными силами. В частности, для рассматриваемой сетчатой оболочки из КМ представим их в виде:

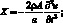
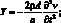(4.22)

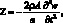
где ρ – плотность материала оболочки.

Для рассматриваемой оболочки с шарнирным опиранием по торцам примем решение системы (4.20) в виде двойных тригонометрических рядов [17]:

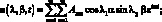
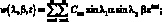(4.23)

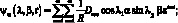
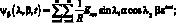
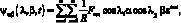
где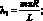

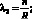
ω –	частота колебаний;
Аmn, Вmn, Сmn, Dmn, Emn, Fmn –	интегральные константы m и n широт и продольных длин волн.

Подставляя решения (4.23) и (4.20) получим систему из шести алгебраических уравнений относительно неизвестных постоянных Аmn, Вmn, Сmn, Dmn, Emn, Fmn.

Видно, что уравнение (4.23) удовлетворяет следующим граничным условиям:

α = 0; α = L; ψβ = 0; Nαβ = 0; w = 0; Mα = 0; Nα = 0.

Существование нетривиальных решений этой системы требуют, чтобы определитель ее был равен нулю, т.е. получим:

(4.24)

где коэффициенты Aij имеют вид:

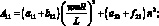
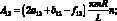
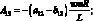
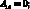
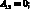
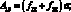
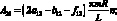
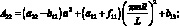
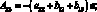
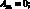
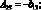
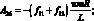
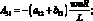
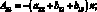
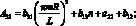
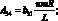
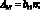
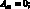
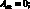
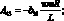
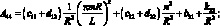
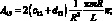
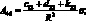
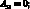
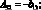
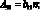
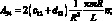
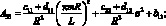(4.25)

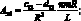
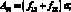
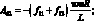
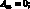
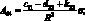
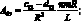
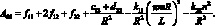
Раскладывая определитель и группируя в нем члены, запишем уравнение для определения частоты собственных колебаний сетчатой цилиндрической оболочки:

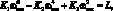(4.26)

где K1, K2, K3 – коэффициенты, определяемые следующими выражениями:

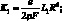
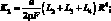(4.27)

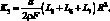
Здесь через L и Li обозначены следующие определители:

(4.28)

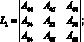
(4.29)

С целью исследования возможных упрощений частотного уравнения (4.26) и для получения конкретных численных результатов проведем параметрический анализ решений.

Оценим влияние угла φ и геометрических параметров оболочки на частоты собственных колебаний. Для этого рассмотрим изгибные колебаний. В этом случае в исходной системе уравнений движения (4.20) описывающих колебательных процесс оболочки, можно положить χ = y = 0. Тогда уравнение для определения частоты колебаний оболочки запишется:

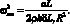(4.30)

Изменения частоты от угла и от параметров оболочки показаны на рис. 4.4–4.6.

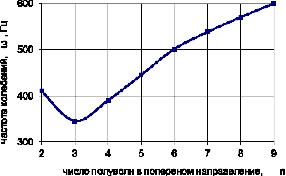
Рис. 4.4

На рис. 4.4.–4.6. приведены зависимости безразмерного параметра частоты от угла φ для различных значений параметров безразмерных длины и толщины оболочки. Пунктиром на рис. 4.4–4.6. показано решение, полученное по алгоритму, разработанному в главе III. Как видно из этих рисунков, в области малых углов φ обе типа решения практический совпадают. Начиная с углов 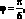решение, полученное на основе
дискретной модели, существенно отличается от решения, полученного по континуальной модели. Это объясняется тем, что при рассмотрении дискретной модели, вводилось допущение о малом угле φ.

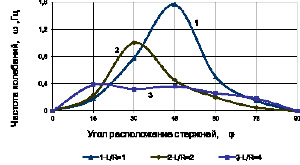
Рис. 4.5

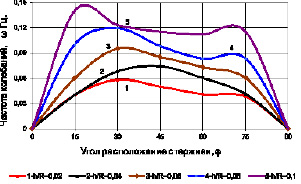
Рис. 4.6