Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

ДИНАМИЧЕСКОЕ ПОВЕДЕНИЕ ОБОЛОЧКИ ИЗ КОМПОЗИЦИОННЫХ МАТЕРИАЛОВ тетрагональнОЙ СТРУКТУРЫ

Немеребаев М. Н., Бекмуратов М. М., Орынбаев С. А., Актаев Е. К.,

4.3. Параметрические колебания сетчатой оболочки из композиционных материалов

Сетчатые оболочки, образованные системой ребер, используются в настоящее время при строительстве сооружений различного назначения. В последние годы геодезические сетчатые конструкции, изготовленные из современных композитных материалов методом намотки,
находят все более широкое применение в ракетно-космической технике. В качестве переходных отсеков ракет, корпусов космических аппаратов и несущих элементов космических платформ, имеющих форму цилиндрических или конических оболочек. Сетчатые композитные оболочки рассматриваются в качестве перспективных элементов конструкций крыла, оперения и фюзеляжа пассажирского самолета, имеющих достаточно сложную форму. В настоящей работе рассматриваются параметрические колебания сетчатых композитных оболочек.

Перейдем к рассмотрению параметрических колебаний сетчатой цилиндрической оболочки из композиционных материалов (КМ) в геометрически нелинейной постановке.

Для этого воспользуемся уравнениями в смешанной форме (4.31), (4.32), пребрегая инерцией вращения и учитывая что радиальная компонента массовой силы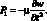

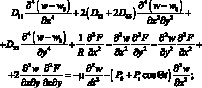(4.31)

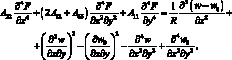(4.32)

Согласно X = 0, L, 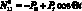будем считать, что при осесимметричных вынужденных колебаниях сетчатой оболочки из КМ возникает безмоментное однородное напряженное состояние, определяемое усилием 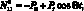которому соответствует функция усилий 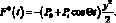Тогда «дополнительная» функция усилий Φ(x, y, t), отвечающая напряженному состоянию сетчатой оболочки из КМ, возникающему при неосесимметричных параметрических колебаниях, равна

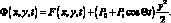(4.33)

В результате подстановки (4.33) система уравнений (4.31), (4.32) принимает вид

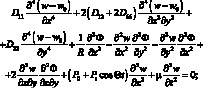(4.34)

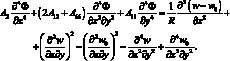(4.35)

Поскольку действующие на торцы сетчатой оболочки из КМ усилия осесимметричны, граничные условия для функции Φ, согласно (4.33), однородны.

Практически все известные решения задачи о нелинейных параметрических колебаниях цилиндрической оболочки [1, 2, 3] получены методом Бубнова-Галеркина.

Корректность и эффективность решений найденных с помощью этого метода, как известно в первую очередь определяются удачным выбором выражений, аппроксимирующих неизвестные функции.

Рассмотрим результаты решения задачи о нелинейных параметрических колебаниях сетчатой цилиндрической оболочки из КМ на основе двучленной аппроксимации прогиба.

(4.36)

где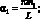

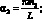
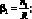
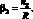
Подстановка (4.36) в уравнение (4.35) дает следующее выражение для функции усилий:

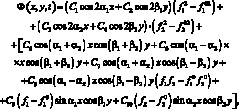(4.37)

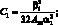
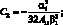
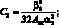
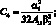
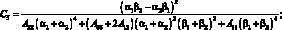
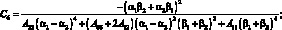(4.38)

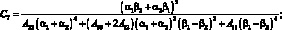
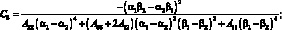
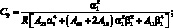
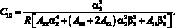
Жескость сетчатой оболочки из КМ Aij определаятся соотношением из (4.19).

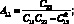
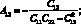
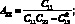
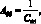
где

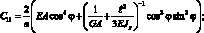
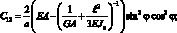
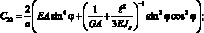
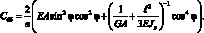
Подставляя далее (4.36) и (4.37) в (4.34) применяя процедуру ортогонализации, приходим к следующей системе двух нелинейных обыкновенных дифференциальных уравнений с периодическими коэффициентами:

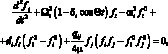(4.39)

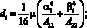(4.40)

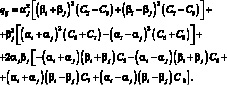(4.41)

В (4.39)–(4.41) i = 1, 2; j = 2 при i = 1 и j = 1 при i = 2. Система (4.39) дополняется начальными условиями при: t = 0:

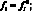
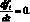(4.42)

Для численного интегрирования задачи Коши (4.39) , (4.42) применяется стандартная программа метода Рунге-Кутта четвертого порядка точности.

Рассмотрим в качестве примера сетчатую оболочку из КМ с характеристиками: R = 1 м, R/h = 100, L/R = 2, φ = 15°, E = 3,5∙1010; μ = 0,3; ρ = 2,5∙103 кг/м3.

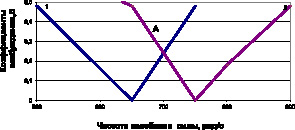
Рис. 4.7. Спектор ОДН сетчатой оболочки из КМ:
1 – m и n {1, 5} ОДН; 2 – m и n {1, 6} ОДН

Обозначим через Ркр минимальное по {m, n} значение осевого критического усилия, введем обозначение 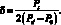В последующих расчетах принято P0 = 0,5Pкр и  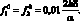На рис. 4.7 отражены результаты численного интегрирования задачи Коши (4.39), (4.42) при
δ = 0,3 и значения θ = 700 рад/с (рис. 4.8, 4.9) В этом случае параметры нагрузки соответствуют точке А (рис. 4.7), находящейся в пересечении двух областей динамической неустойчивости (ОДН) для формы колебаний {1, 5} и {1, 6}. Как видно, в этом случае наблюдается параметрический резонанс по обеим формам.

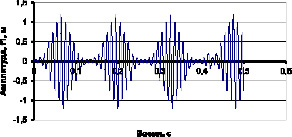
Рис. 4.8. Зависимость изменения амплитуды f1 по времени

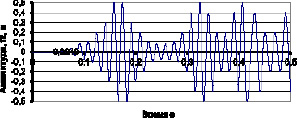
Рис. 4.9. Зависимость изменения амплитуды f2 по времени

Изложенная методика расчета, основанная на двучленной аппроксимации прогиба (4.36), может быть обобщена на случай большего числа взаимодействующих пространственных гармоник. При этом систему, обобщающую (4.39), достаточно вывести для случая трех гармоник. Дальнейшее обобщение элементарно проводится по индукц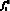ии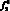.