Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

ДИНАМИЧЕСКОЕ ПОВЕДЕНИЕ ОБОЛОЧКИ ИЗ КОМПОЗИЦИОННЫХ МАТЕРИАЛОВ тетрагональнОЙ СТРУКТУРЫ

Немеребаев М. Н., Бекмуратов М. М., Орынбаев С. А., Актаев Е. К.,

4.4. Динамическая устойчивость сетчатой оболочки из композиционных материалов

Большое практическое значение имеет расчет колебаний оболочек в случае, когда сжимающая осевая сила представляет собой периодическую функцию по времени. Возникающие при этом поперечные колебания являются параметрическими, они имеют своеобразные черты, существенно отличающие их от обычных вынужденных колебаний оболочек, они могут быть динамически устойчивыми или неустойчивыми [21, 39].

В данной работе рассмотрена следующая задача: пусть сетчатой оболочки из композиционных материалов нагружена периодически изменяющимися тангенциональными силами с малыми амплитудами, приложенными в срединной поверхности. В этом случае, при определенных соотношениях между частотой собственных колебаний, начальная форма оболочки становится динамически неустойчивой.

Ставится цель приближенно определить границу первой области неустойчивости оболочки тетрагональной структуры. Для простоты, как в [5], предположим, что начальное напряженное состояние является безмоментным и характеризуется тангенциальной силой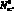

Тангенциональные силы инерции, силу инерции вращения и деформацию поперечных сдвигов в расчетах не учитываем. На основе выше изложенного из [29] с учетом 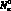получим

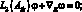(4.43)

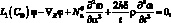
где

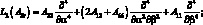
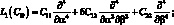(4.44)

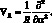
Для решения системы (4.43) применяем вариационный метод. Тогда уравнение (4.43) принимает вид:

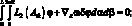
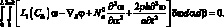(4.45)

Решением этой системы является:

φ(α, β, T) = Фmn(t)φmn(α, β);

ω(α, β, t) = Fmn(t)ωmn(α, β). (4.46)

φmn(α,β) и ωmn(α,β) представим в виде проиведения двух функций, каждая из которых зависит только от одного аргумента и может быть представлена в виде линейных комбинаций фундементальных функций поперечных колебаний балок, заведомо удовлетворяющих только двум граничным условиям на каждом краю оболочки.

φmn(α, β) = Xm(α)Yn(β);

ωmn(α, β) = Um(α)Vn(β). (4.47)

Выразим решение (4) в следующем виде:

δφ = φmnδФmn; δω = ωmnδFmn. (4.48)

Вариации коэффициентов Фmn и Fmn, являющихся функциями лишь времени (t) произволны и не связаны между собой. Используя произвольность вариации δФmn и δFmn, а также ортогональность фундаментальных функций

Xm(α), Yn(β), Um(α) и Vn(β) согласна (4.43), (4.44) и (4.48) получим следующую систему уравнений:

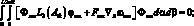
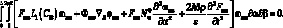(4.49)

где m = 1, 2, 3; n = 1, 2, 3.

Подставля значения φmn и ωmn из (4.45) в систему (4.49) и вычисля соответствующие интегралы, получим систему уравнений относительно функции Фmn(t) и Fmn(t). Затем, исключив из системы Фmn(t) получим следующее уравнение, относительно Fmn(t):

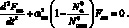(4.50)

Здесь введены следующие обозначения:

для квадрата частот собственных колебаний оболочек

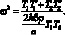(4.51)

для критических значений тангенциальной силы при ее независимом статическом действии

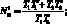(4.52)

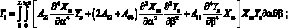(4.52)

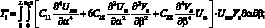(4.53)

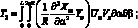(4.54)

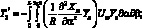(4.55)

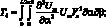(4.56)

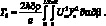(4.57)

Пусть оболочка шарнирного оперта. Тогда граничные условия имеют вид:

α = 0; ω0 = 0; M1 = 0; Nα = 0; V = 0. (4.58)

В этом случае, полагая

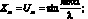
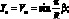
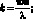
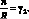(4.59)

из (4.51) и (4.52) согласно (4.53)–(4.57) и (4.59), получим для коэффициентов уравнения (4.50) следующие выражения

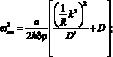(4.60)

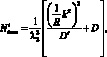(4.61)

где

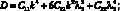(4.62)

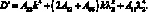
Принимая 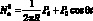, получим из уравнения динамической устойчивости уравнение параметрических колебаний:

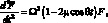(4.63)

где

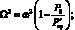
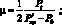
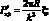
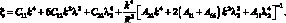
Рассмотрим решение задачи с учетом силы сопротивления. Для этого положим, что сила сопротивления является линейной функцией скорости перемещения, с коэффициентом линейного затухания ε. Перепишем уравнение (4.63) следующим образом

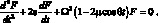(4.64)

Формула определения границ главной области неустойчивости можно представить в виде [1, 3]

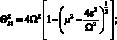
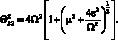(4.65)

Нетрудно видеть, что при симметрической форме потери устойчивости n = 0, а критическая частота Θk принимает минимальное значение при

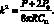(4.66)

Тогда верхняя и нижняя границы неустойчивости (при ε = 0) имеет вид:

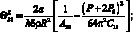
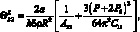(4.67)

где согласно(4.19)

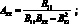
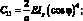
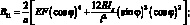(4.68)

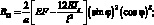
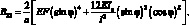
Принимая во внимание (4.68) и проводя несложные преобразования перепишем формулу (4.67) в виде:

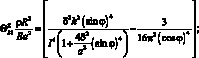
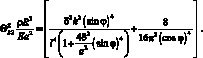(4.69)

Здесь принято: P0 = 0; P = Ehδ.

Проведенный численный анализ показывает, что:

● Минимальные значения ширины зоны устойчивости находятся в окрестностях φ = 0. Вблизи угла 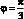происходит бурное возрастание критических частот, а в окрестностях 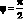происходит разрыв критических частот. Это объясняется тем, что полученое решение (4.69) имеет особенность при углах (φ = 0 и )

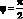● Оболочка с углом φ = 0 представляет собой систему продольных ребер. В том случае, как видно из (4.68), B12 = 0, B22 = 0. При этом получим известные выражения, определяющие динамическую устойчивость шарнирно закрепленного стержня [39].

● Оболочка с углом 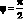вырождается в систему колец, которые не воспринимают осевую периодическую нагрузку.