Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

ПРИЁМ И ОБРАБОТКА СИГНАЛОВ ОТ СЛОЖНЫХ ЦЕЛЕЙ

Доросинский Л. Г., Трухин М. П.,

3.1. Методика использования граничных соотношений Чернова и Кайлата для оценки эффективности классификации ПРЦ по вектору наблюдаемых данных

Потенциальные возможности решения задачи многоальтернативной проверки гипотез (а именно в таком виде формализуется задача распознавания ПРЦ) в подавляющем большинстве практических случаев характеризуются вероятностями вынесения правильных (Рпр) и ошибочных (Рош) решений. Точный аналитический расчет этих вероятностей может быть выполнен лишь в простейших частных случаях. В большинстве реальных радиолокационных ситуаций практически единственным методом оценки эффективности распознавания является метод статистического моделирования (математического, натурного и т. п.). Однако, на этапе эскизного проектирования, предварительной оценки, прогноза эффективности, когда необходимо оценить принципиальную возможность функционирования проектируемых алгоритмов и произвести выбор основных параметров РЛС, использование даже гибкого математического моделирования приводит к недопустимым затратам машинного времени в связи с чрезвычайно большим количеством анализируемых (перебираемых) параметров. В этих условиях для получения количественных оценок вероятностных характеристик работы системы наиболее целесообразным следует признать использование граничных соотношений Чернова и Кайлата [1, 2, 7], которые были введены для случая проверки двух гипотез и в данной работе распространены на произвольное их количество.

При проверке (М + 1) гипотез вероятность вынесения ошибочного решения равна:

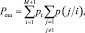(3.1.1)

где рi – априорная вероятность i-й гипотезы; p(j/i) – вероятность вынесения решения в пользу j-й гипотезы в том случае, когда истинной является 1-я гипотеза.

Это выражение можно представить в виде:

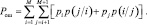(3.1.2)

В дальнейшем предполагаем, что решение в пользу того или иного класса принимается с использованием критерия минимума полной вероятности ошибки.

Используя методику [1], можно найти верхнюю границу ошибки (3.1.2) при проверке многих гипотез:

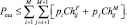(3.1.3)

В последнем выражени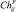и и 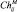 – границы Чернова для вероятностей ложной тревоги и пропуска цели при проверке пары гипотез i и j независимо от остальных гипотез.

Необходимо отметить, что оценка ошибки, даваемая неравенством (3.1.3), может быть существенно завышена, причем точность оценки в общем случае уменьшается по мере увеличения числа конкурирующих гипотез.

В этих условиях представляется безусловно целесообразным нахождение и нижней границы вероятности ошибки правильной классификации (3.1.1). Для бинарного обнаружения такая граница введена Кайлатом [3]. В данной работе произведено обобщение названной границы на случай произвольного числа гипотез.

Для отыскания нижней границы вероятности ошибки воспользуемся выражением (3.1.1). Сумма по j в его правой части представляет собой вероятность вынесения ошибочного решения при наблюдении цели i-го класса. Такая ошибка возникает, если хотя бы для одной из альтернативных гипотез выполняется неравенство:

lij > lii (i ≠ j), (3.1.4)

в котором

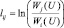(3.1.5)

– логарифм отношения правдоподобия при проверке пары гипотез с номерами j и i; Wj(U) и Wi(U) – плотности распределения вероятностей значений вектора наблюдаемых данных U по гипотезам j и i. Пусть событие Аj соответствует выполнению условия (3.1.4). Тогда вероятность ошибки при наблюдении i-го класса целей представляется как вероятность суммы событий:

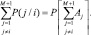(3.1.6)

Используя формулу для определения вероятности суммы зависимых событий [4], можно убедиться в справедливости неравенства:

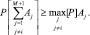(3.1.7)

В этом выражении р[Aj] представляет собой вероятность вынесения решения в пользу j-гo класса целей при условии, что истинной является цель i-го класса при проверке только этой пары альтернатив. Обозначая эту вероятность P2(j/i) и используя (3.1.7), для вероятности ошибки (3.1.1) запишем неравенство:

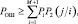(3.1.8)

где на значение j наложено единственное ограничение:

j ≠ i. (3.1.9)

Неравенство (3.1.8) позволяет оценить нижнюю границу вероятности ошибки в случае проверки более двух гипотез. Поскольку нас, в первую очередь, интересует случай распознавания трех классов, сосредоточим внимание именно на этой задаче (обобщение на произвольное число классов производится аналогично).

Используя (3.1.8) и (3.1.9), запишем два очевидных неравенства:

PОШ ≥ P1P(2/1) + P2P2(3/2) + P3P2(1/3);

PОШ ≥ P1P(3/1) + P2P2(1/2) + P3P2(2/3). (3.1.10)

Суммируя правые и левые части этих неравенств, получим:

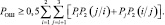(3.1.11)

Выражение, стоящее в квадратных скобках (3.1.11), представляет собой вероятность ошибки при решении задачи проверки двух гипотез – i-й и j-й. Для оценки этой ошибки воспользуемся методикой, предложенной в [1]. При этом необходимо помнить, что в нашей постановке гипотезы с номерами i и j не образуют полной группы событий, то есть

Pi + Pj ≠ 1. (3.1.12)

Используя критерий минимума ошибки, искомую вероятность графически можно представить в виде суммы заштрихованных на рис. 3.1 площадей С и D (на этом рисунке изображены апостериорные плотности вероятностей для двух рассматриваемых гипотез). В соответствии с рисунком можно записать два равенства:

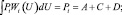
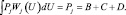(3.1.13)

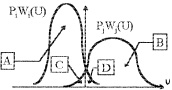
Рис. 3.1. К вопросу о нижней границе вероятности ошибки

Суммируя их, получим:

А + В + 2(С + D) = Pi + Рj. (3.1.14)

Нетрудно заметить, что:

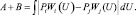(3.1.15)

Следовательно, искомая вероятность ошибки равна:

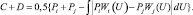(3.1.16)

Для оценки интеграла (3.1.15) применим неравенство Шварца [4]:

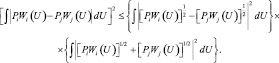(3.1.17)

После преобразования правой части (3.1.17) получим:

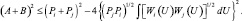(3.1.18)

Следовательно

PiP2(j/i) + PjP2(i/j) = C + D ≥ Klij, (3.1.19)

где 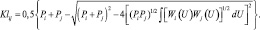(3.1.20)

Это выражение можно представить в виде:

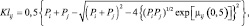(3.1.21)

где 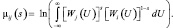(3.1.22)

Выражение (3.1.21) представляет собой обобщение границ Кайлата для двух гипотез i и j, не образующих полной группы событий.

Окончательно (3.1.11) запишем в виде

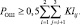(3.1.23)

По аналогии с (3.1.10) и (3.1.11) можно найти нижнюю границу вероятности ошибки для любого числа конкурирующих гипотез. В общем случае проверки М + 1 гипотез имеем:

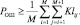(3.1.24)

Приведенные выше выкладки получены для случая, когда наблюдаемые данные представляют собой скалярную величину. Однако, все результаты справедливы, если наблюдаемые данные имеют векторный характер. Изменения при этом затрагивают только выражение (3.1.22) для логарифма производящей функции моментов, которое принимает следующий вид:

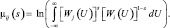(3.1.25)

Для расчета границ Чернова 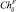и 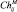 воспользуемся методикой, описанной в [5] и основанной на разложении в ряд Эджворта плотности вероятности, которая предполагается близкой к гауссовской. Ограничиваясь двумя первыми членами разложения, имеем:

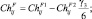(3.1.26)

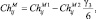(3.1.27)

где 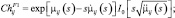(3.1.28)

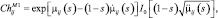(3.1.29)

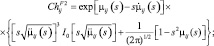(3.1.30)

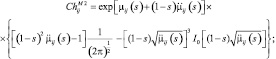(3.1.31)

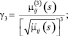(3.1.32)

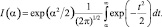(3.1.33)

Значение аргумента s в (3.1.29)–(3.1.32) находится путем решения уравнения

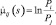(3.1.34)

Как следует из выражений (3.1.21), (3.1.29)–(3.1.32), для определения верхней и нижней границ вероятности вынесения ошибочного решения (3.1.1) требуется знать функцию µij(s) и ее три первые производные для всех возможных пар распознаваемых классов целей.

Для расчета необходимых выражений воспользуемся (3.1.25), предполагая, что вектор наблюдаемых данных U представляет собой совокупность комплексных гауссовских отсчетов с нулевыми средними значениями. При этом для µij(s) может быть получено следующее выражение:

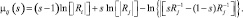(3.1.35)

где Ri и Rj – корреляционные матрицы вектора Y по гипотезам i и j соответственно. Для вычисления значений правой части выражения (3.1.35) обычно используют теорему Кейли-Гамильтона [6]. Однако, ее непосредственное применение к (3.1.35) требует нахождения собственных значений трех различных матриц для каждой пары гипотез. Процедура поиска собственных значений является достаточно трудоемкой. Для ее упрощения целесообразно разложить эрмитову матрицу Rj на множители по Холецкому:

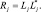(3.1.36)

где Lj – нижняя (левая) треугольная матрица, а символ * обозначает эрмитово сопряжение.

При этом выражение (3.1.35) может быть представлено в виде:

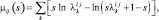(3.1.37)

где 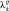 – k-е собственное значение матрицы:

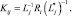(3.1.38)

Искомые производные функции μij(s) имеют вид:

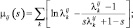(3.1.39)

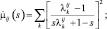(3.1.40)

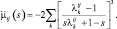(3.1.41)

Из приведенных соотношений следует, что в рассматриваемой постановке граничные значения вероятности ошибки при многоальтернативной проверке гипотез полностью определяются корреляционными матрицами отсчетов вектора наблюдаемых данных по каждому из возможных классов.

Определим вид этих матриц, считая, что входящие в систему РЛС независимы между собой. Последнее предположение позволяет ограничиться рассмотрением корреляционной матрицы отсчетов РЛИ, получаемого в отдельной р-й РЛС системы при наблюдении k-й цели.

Таким образом, РЛИ цели можно представить в виде суммы трех составляющих: шумовой

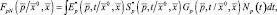(3.1.42)

диффузионной

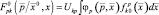(3.1.43)

и составляющей, вызванной наличием «блестящих точек» в составе модели ПРЦ k-го класса:

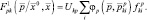(3.1.44)

Эти составляющие независимы между собой, и, следовательно, элементы искомой корреляционной матрицы представимы в виде суммы:

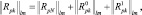(3.1.45)

где 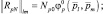(3.1.46)

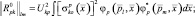(3.1.47)

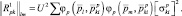(3.1.48)

Дискретные значения и 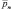 задают координаты отсчетов РЛИ на плоскости изображения.

Функции неопределенности траекторного сигнала 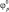и φр определяются в соответствии с (3.3.19).

Вводя нормированные функции неопределенности 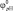и φрН и пренебрегая константами, не влияющими на вычисление функции µij(s) и ее производных, выражение (3.1.45) можно представить в следующем виде:

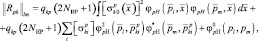(3.1.49)

где 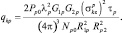(3.1.50)

представляет собой эквивалентное отношение энергии сигнала к спектральной плотности шума в импульсе для случая наблюдения точечного отражателя с ЭПР, равной суммарной ЭПР цели (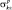)2, при расположении его в точке, соответствующей центру цели. Выражение

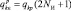(3.1.51)

следует рассматривать как суммарное отношение сигнал/шум по пачке из (2NИ + 1) импульсов.