Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
7.4.1. Одинаковые Pi
Упростим оптимальный алгоритм обнаружения дружно движущейся ПРЦ (6.15) при больших отношениях сигнал/шум, отказавшись от операции экспонирования, как это было сделано ранее. Тогда квазиоптимальный алгоритм примет вид:
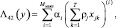 (7.65)
(7.65)
где операция ( )(i) означает нахождение i-й порядковой статистики. Максимальное время на формирование Λ42 равно
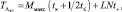
машинная память составляет 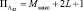 ячеек.
ячеек.
Определим вероятность ложной тревоги алгоритма (7.65) в наиболее простом случае: ρi = 1, 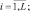 N = 1. Совместная плотность вероятности всех L порядковых статистик имеет вид [17]:
N = 1. Совместная плотность вероятности всех L порядковых статистик имеет вид [17]:
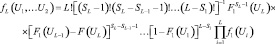 (7.66)
(7.66)
где F1(•) – функция распределения случайных величин, из которых образуется вариационный ряд или генеральная функция распределения; f1(•) – генеральная плотность вероятности; SL – номер порядковой статистики.
В данном случае SL образует натуральный ряд от 1 до L, поэтому
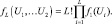 (7.67)
(7.67)
Многомерная характеристическая функция, соответствующая совместной плотности вероятности (7.67), определяется прямым L-мерным преобразованием Фурье:
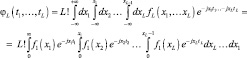 (7.68)
(7.68)
Здесь нижние пределы у интегралов равны нулю, поскольку случайные величины xi ≥ 0. При релеевском распределении амплитуд отраженных сигналов генеральное распределение F1(•) является экспоненциальным, характеристическая функция которого φ1(t) = 1/(1 + jt).
Проведем вычисление φL(t1, …, tL) последовательно, начиная со значения L = 1, при котором φ1(t1) = φ1(t) = (1 + jt)–1.
При L = 2
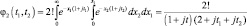 ;
;
при L = 3
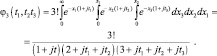
Методом математической индукции можно показать, что в общем случае
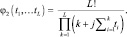 (7.69)
(7.69)
Поставив вместо ti в (7.67) 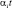 , получим характеристическую функцию взвешенных сумм L порядковых статистик при отсутствии отраженных сигналов:
, получим характеристическую функцию взвешенных сумм L порядковых статистик при отсутствии отраженных сигналов:
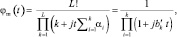 (7.70)
(7.70)
где 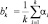 .
.
Вероятность ложной тревоги определяется интегралом в пределах от T до ∞ от обратного преобразования Фурье от функции (7.70):
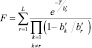 , (7.71)
, (7.71)
которое по форме совпадает с (7.15). Процедура FIN, с помощью которой для заданной F находится порог T, приведена в [2].
Определим вероятность правильного обнаружения алгоритма (7.65) при названных выше условиях и разрешенных сигналах от отдельных элементов ПРЦ. Обозначим парциальной многомерной характеристической функцией характеристическую функцию ситуации, когда имеется M сигнальных и L – M шумовых отсчетов в вариационном ряду. Положение членов вариационного ряда, создаваемых сигнальными отсчетами, среди шумовых жестко фиксировано. Перестановки только среди шумовых или среди сигнальных отсчетов не меняют вида парциальной характеристической функции. Таких перестановок имеется M!(L – M)! Перестановки же среди разнородных членов вариационного ряда при одинаковом их числе изменяют вид парциальной характеристической функции. Число разнородных перестановок равно 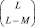 Общая характеристическая функция равна сумме парциальных функций:
Общая характеристическая функция равна сумме парциальных функций:
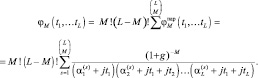 (7.72)
(7.72)
Здесь 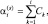 где Ck = 1, если на k-м месте в вариационном ряду стоит шумовой отсчет, и Ck = (1 + g)–1, если на этом месте стоит сигнальный отсчет. Верхний индекс s означает одно из возможных сочетаний. Методика получения (7.72) аналогична использованной выше. Характеристическая функция распределения статистики Λ42 при наличии отраженных сигналов записывается на основании выражения (7.72):
где Ck = 1, если на k-м месте в вариационном ряду стоит шумовой отсчет, и Ck = (1 + g)–1, если на этом месте стоит сигнальный отсчет. Верхний индекс s означает одно из возможных сочетаний. Методика получения (7.72) аналогична использованной выше. Характеристическая функция распределения статистики Λ42 при наличии отраженных сигналов записывается на основании выражения (7.72):
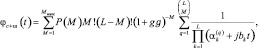 (7.73)
(7.73)
где 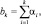
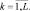
Вероятность правильного обнаружения находится обратным преобразование Фурье от φс+ш(t) и интегрированием в пределах от T до ∞:
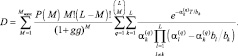 (7.74)
(7.74)
Практические расчеты характеристик обнаружения с использованием (7.74) связаны с большими трудностями. Произведение, стоящее в знаменателе, велико по абсолютной величине и знакопеременно, поэтому уже при L и Mмакс > 8 ошибки округления настолько велики, что единственным методом отыскания характеристик обнаружения является метод статистического моделирования.
Найдем вероятность ложной тревоги алгоритма (7.65) при ρi = 1 и произвольном N для релеевской модели отраженных сигналов. В этом случае генеральным распределением является γ-распределение 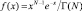 . Воспользуемся возможностью дифференцирования выражения (68) по параметру. Многомерная производная от характеристической функции φL(t1, …, tL) равна:
. Воспользуемся возможностью дифференцирования выражения (68) по параметру. Многомерная производная от характеристической функции φL(t1, …, tL) равна:
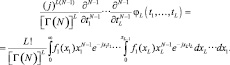 (7.75)
(7.75)
Если принять 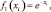 то (7.75) совпадает с характеристической функцией φL(t1, …, tL) распределения Λ42 при произвольном значении N. Обозначим
то (7.75) совпадает с характеристической функцией φL(t1, …, tL) распределения Λ42 при произвольном значении N. Обозначим
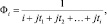
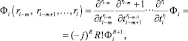
где 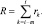
Тогда многомерная характеристическая функция имеет вид:
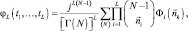 (7.76)
(7.76)
где векторы 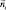 и
и 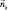 являются соответствующими строками и столбцами целочисленной матрицы
являются соответствующими строками и столбцами целочисленной матрицы
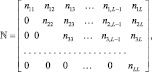
в которой сумма элементов каждой строки равна N – 1; nik = 0, k < i. В (7.76) сумма берется по всем возможным наборам {N} чисел, записанным в матрице ¥. Таким образом, вероятность ложной тревоги равна
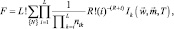 (7.77)
(7.77)
где k = L;