
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
7.4.2. Неодинаковые Pi
Определим также вероятность ложной тревоги при N = 1 и различных Pi. Многомерная характеристическая функция φL(t1, …, tL) находится тем же методом, что и в начале пункта:
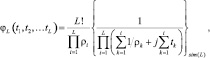 (7.78)
(7.78)
где символ {.}sim(L) обозначает операцию симметрирования [18] стоящей в фигурных скобках функции относительно аргументов ρk и tk. Число аргументов указано после знака sim. Тогда величина F для этого случая определяется согласно выражения:
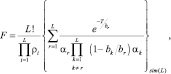 (7.79)
(7.79)
где 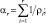
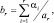 а симметрирование проводится дружно по всем L значениям αi и ρi.
а симметрирование проводится дружно по всем L значениям αi и ρi.
Определение вероятности ложной тревоги по выражениям (7.77) и (7.79) можно проводить при малых L. При N > 8 следует использовать гауссовскую аппроксимацию для суммы 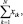 предполагая тем самым, что генеральное распределение является нормальным N(N, N).
предполагая тем самым, что генеральное распределение является нормальным N(N, N).
Отыскание точных аналитических выражений для F в общем случае и D для условий, использованных при вводе (7.77) и (7.79), следует признать нецелесообразным, поскольку большая сложность формул делает невозможным расчет F и D при L > 4.
Методом статистического моделирования (Q = 1000) были получены численные характеристики обнаружения алгоритма (7.65) при ρi = 1, 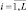 , и весовых коэффициентах αi = ci, образующих геометрическую прогрессию [2]. Графики характеристик, изображенные на рис. 7.38 и 7.39 и помеченные цифрами 6, 7, 8, 9 соответствуют показателям прогрессии c = 0,1; 0,2; 0,5; 0,8. Проведен также анализ случая c = 0,9. Для сравнения на этих рисунках построены характеристики обнаружения алгоритмов с накоплением (обозначена цифрой 1) и выбором максимума (обозначена цифрой 5). Графики построены для случаев, когда различие между характеристиками может быть представлено графически.
, и весовых коэффициентах αi = ci, образующих геометрическую прогрессию [2]. Графики характеристик, изображенные на рис. 7.38 и 7.39 и помеченные цифрами 6, 7, 8, 9 соответствуют показателям прогрессии c = 0,1; 0,2; 0,5; 0,8. Проведен также анализ случая c = 0,9. Для сравнения на этих рисунках построены характеристики обнаружения алгоритмов с накоплением (обозначена цифрой 1) и выбором максимума (обозначена цифрой 5). Графики построены для случаев, когда различие между характеристиками может быть представлено графически.

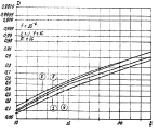
а б
Рис. 7.38. Характеристики обнаружения алгоритмов (7.16), (7.55) и (7.65)
при равномерном (а) и малоэлементном (б) априорных распределениях


а б
Рис. 7.39. Характеристики обнаружения алгоритмов (7.16), (7.55) и (7.65) при многоэлементном априорном распределении:
а – m = 8; б – m = 16
Из всех приведенных ситуаций обнаружения лишь при равномерном распределении числа элементов алгоритм (7.65) обнаруживает ПРЦ лучше других (при 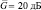 ), но различие между ними и алгоритмом с накоплением (1) невелико и равно примерно 0,2 дБ (см рис. 7.39, а, кривая 9). Во всех остальных ситуациях алгоритмы по качеству обнаружения
), но различие между ними и алгоритмом с накоплением (1) невелико и равно примерно 0,2 дБ (см рис. 7.39, а, кривая 9). Во всех остальных ситуациях алгоритмы по качеству обнаружения
расставляются в такой последовательности: 1, 10, 9, 8, 7, 6 и 5. Крайними, как и следовало ожидать, являются алгоритмы (6.16) и (7.55), алгоритм (7.65) с различными значениями c занимает между ними соответствующие промежуточные положения.
При c ≥ 0,8 алгоритм (7.65) близок к алгоритму (6.16), при c ≤ 0,2 – к алгоритму (7.55). Лишь в диапазоне изменений показателя геометрической прогрессии от 0,4 до 0,6 (кривая 8) наблюдается более резкая зависимость D от c. Следует отметить, что использование других законов изменения коэффициентов αi, например, таких, какие приведены в начале параграфа, приводит к несущественному относительному сдвигу характеристик обнаружения алгоритма (7.65), соответствующему второму порядку малости взаимных проигрышей и выигрышей в пороговом сигнале.
Итак, использование алгоритма с порядковой статистикой в рассмотренных ситуациях обнаружения не дает практически никаких выигрышей в пороговом сигнале и от него вполне можно отказаться. Этот вывод тем более справедлив еще и потому, что реализация алгоритмов с использованием порядковых статистик наталкивается большие вычислительные трудности.
