Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Применение метода исключения варьируемого параметра при решении задач диагностирования

Портнягин Н. Н., Пюкке Г. А.,

2.3. Упорядочение и минимизация множества основных диагностических признаков

Элементы полученного множества основных диагностических признаков имеют различную чувствительность к вариациям параметров диагностируемых компонент. Эта чувствительность зависит от выбора канала диагностирования, топологии и физической особенности ОД. При разработке диагностического обеспечения  необходимо получить зависимость чувствительности различных каналов диагностирования к вариациям параметров всех компонент ОД и определить наиболее чувствительные диагностические признаки для дальнейшего включения их в модель диагностирования. [40, 7]. В качестве критерия чувствительности могут быть использованы частные производные вида:

S _{i j} = ¦K _{i j} ¦ / ¦g _k¦,

где K _{i j} – функция  передачи от i – го  входа к j – му  выходу; g_k – параметр  структурной единицы. Произведя оценку чувствительности каждого диагностического параметра, все множество можно упорядочить по чувствительности, результаты представить двумерным массивом  (табл. 2.2.).

Таблица 2.2. Чувствительностей каналов диагностирования

.

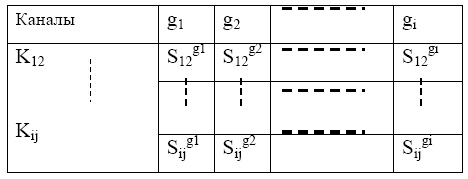Каждый вертикальный столбец таблицы будет представлять собой совокупность чувствительностей функций передачи К_ij относительно изменений одного и того же параметра СЕ g_i. Каждая строка будет представлять собой чувствительность одной и той же функции передачи К_ij относительно изменений всех g_i. Представление информации таким способом позволяет легко формализовать процедуру анализа чувствительности и выбора совокупности наиболее информативных диагностических признаков по критериям чувствительности и равномерности чувствительности к изменению всех g_i. После этого все признаки можно упорядочить, поставив на первое место наиболее чувствительные. Величина чувствительности, рассматриваемого диагностического признака, в общем случае, не является величиной постоянной, поэтому при подсчете чувствительностей численные значения производных следует искать в точке g_i = g_i ном. Однако этого критерия недостаточно для анализа чувствительностей всех каналов прохождения тестового сигнала, т.к. с ростом размерности диагностируемой электрической цепи может уменьшаться чувствительность некоторых функций передачи к вариациям проводимостей СЕ, принадлежащих гальванически слабосвязанным подцепям. Поэтому отбор функций передачи производится еще и по равномерности чувствительности, выбранных функций передачи к вариациям проводимостей всех СЕ. Для оценки равномерности чувствительности выбранных диагностических признаков используются числовые характеристики случайных величин.  Рассматривая появление различных чувствительностей S ₁, S ₂, …….S _n различных функций передачи как события равновероятные Р₁ = Р₂ = ……= Р_n = 1 / n, а чувствительности функций передачи S_ij, представляющих собой набор детерминированных величин, как различные проявления одной и той же случайной величины, колеблющейся около своего математического ожидания М{S}, выбираем дисперсию D{S}, как величину характеризующую степень рассеяния величины S вокруг М{S}. Тогда дисперсия будет использоваться для оценки равномерности чувствительности диагностических параметров. Здесь Р₁, Р₂ , …….Р_n  - вероятности появления величин S ₁, S ₂, …….S _n. Тогда D {S } = ( S _i – M {S})² P_i . При такой оценке по критериям чувствительности М{S} и равномерности D{S} решается задача отбора подмножества функций передачи, имеющих наибольшую чувствительность и наименьшую неравномерность или среднеквадратическое отклонение σ, имеющее ту же размерность, что и S.

При отборе минимального множества основных диагностических признаков для диагностирования методом изовар необходимо, кроме назван ных критериев по чувствительности и равномерности, удовлетворить требо вание по достаточно низкой инцидентности (совмещенности) изовар. В про­тивном случае разрешающая способность метода снижается. С этой целью мно жество функций передачи минимизируется по критерию эквидистантности изовар. Плохая эквидистантность делает неразличимыми состояния по данным g_k и g_n параметрам. Это имеет место при использовании пар каналов, для которых  отношения  конечно - разностных  производных Δ K₁ / Δ K ₂ по соответствую щим параметрам Δ g _k и Δ g _N  в точках их номинальных значений   g _{k ном} и g _{N  ном}  пропорциональны или совпадают. Поэтому множество основных  диагностических признаков подлежит анализу на эквидистантность  изовар.  Как показали  исследования,  при разработке диагностических моделей на различных ОД, наиболее адекватными критериями отбора подмножества оптимальных функций передачи являются следующие:

1. Комплексный критерий Z оценки интегральных величин чувствительности и равномерности по совокупности каналов:

Z =  max { ² –  M  σ }