
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания

Применение метода исключения варьируемого параметра при решении задач диагностирования
Портнягин Н. Н., Пюкке Г. А.,
2.6. Исследование поведения диагностико-регулировочной модели электрической цепи при вариации параметров диагностируемой системы
Рассмотрим движение точки состояния в пространстве диагностирования при поэтапной вариации всеми m параметрами. Процесс перемещения точки текущего состояния (из п. 1 в п. 2, Рис. 2. 20) при вариации диагностируемого параметра gi описывается одним из соотношений системы (2. 3)
Тав – cd |gi = var = Gi (Тkp – hl ), i = z, a1 ![]() gi
gi ![]() b1, i = 1, 2, …,z,….m,
b1, i = 1, 2, …,z,….m,
где а1, b1 – cooтветственно, нижняя и верхняя границы изменения параметра gi . z – номер варьируемого параметра. В точке 2 значение варьируемого параметра gi |i = z достигает предельной величины gi = b1. При вариации следующим параметром gi |i = z + 1 траектория перехода точки состояния из положения 2 в положение 3 описывается новым соотношением
описывающем траекторию движения точки состояния при вариации z + 1 – го параметра, но не имеющем предисторию вариации z – го параметра.
После вариации всеми m параметрами в пределах ai ![]() gi
gi ![]() bi , i = 1, m , cистема (2. 3) преобразуется в новую систему, содержащую информацию о предистории в виде измененных коэффициентов полиномов аналитических соотношений функций передачи каналов диагностирования
bi , i = 1, m , cистема (2. 3) преобразуется в новую систему, содержащую информацию о предистории в виде измененных коэффициентов полиномов аналитических соотношений функций передачи каналов диагностирования
Тав – cd |gi = var = Gi откл. (Тkp – hl ), i = z + 1, a2 ![]() gi
gi ![]() b2,
b2,
отличным от аналогичного соотношения системы (2. 3)
Тав – cd |gi = var = Gi (Тkp – hl ), i = z + 1,
Тав – cd |g1 = var = G1 (Тkp – hl );
Тав – cd |g2 = var = G2 откл (Тkp – hl );
………………………………
Тав – cd |gm = var = Gm откл (Тkp – hl ). (2. 4)
Изменение порядка вариации диагностируемых параметров gi позволяет получить m! маршрутов движения точки состояния в пространстве диагностирования {Тав – cd , Тkp – hl }. Это дает возможность получить m! различных вариантов системы (2. 4), описывающих движение точки состояния в пространстве диагностирования. Конечного (m + 1) – го состояния можно достичь различными сочетаниями вариаций параметров gi и величин их изменения. При количестве варьируемых параметров равном r и m потенциально возможных маршрутах передвижения точки состояния (количество степеней свободы), количество различных вариантов передвижения точки определяется комбинаторно и составляет Amr = m(m – 1)(m – 2)…….(m – r + 1), где Amr – количество размещений из m элементов по r. Для каждого конечного положения точки состояния, при заданной кратности дефекта, можно указать область всевозможных маршрутов передвижения. Количество всевозможных маршрутов достижения одного из конечных состояний определяется комбинаторно: Е = r!. Количество всевозможных сочетаний варьируемых изовар равно: Д = Cmr , где m- количество изовар, r- количество одновременно варьируемых параметров.
Так как каждое сочетание дает новое конечное состояние, то для системы, состоящей из m СЕ, достижение одного из конечных состояний возможно по одному из r! маршрутов, каждый из которых имеет положительное или отрицательное направление в зависимости от направления отклонения параметра СЕ. Следовательно, количество конечных состояний для одного сочетания варьируемых изовар, с учетом направления отклонения параметра равно: М = 2r, а общее количество конечных состояний, при заданной кратности дефекта, равно: N = Сmr ![]() 2r , которому будет соответствовать R = Cmr
2r , которому будет соответствовать R = Cmr![]() 2r
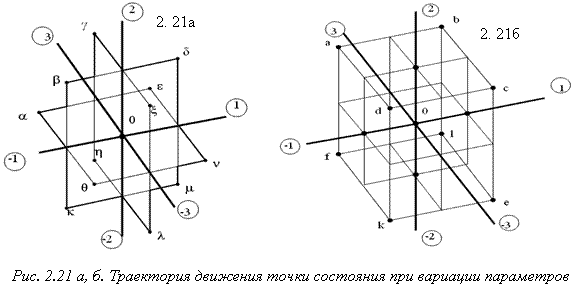
2r ![]() r! различных маршрутов движения точки состояния. На рис. 2. 21 изображены области всевозможных маршрутов движения точки состояния при вариации соответственно трех рис. 2. 21а и двух рис. 2. 21б параметров на упрощенной трехизоварной системе, где : a, b, c, d, e, k, f, l – точки предельных конечных состояний при вариации трех параметров одновременно, а точки α, β, γ, δ, ε, ζ, η, θ, κ, λ, μ, ν - соответствуют конечным состояниям при вариации двух параметров одновременно.
r! различных маршрутов движения точки состояния. На рис. 2. 21 изображены области всевозможных маршрутов движения точки состояния при вариации соответственно трех рис. 2. 21а и двух рис. 2. 21б параметров на упрощенной трехизоварной системе, где : a, b, c, d, e, k, f, l – точки предельных конечных состояний при вариации трех параметров одновременно, а точки α, β, γ, δ, ε, ζ, η, θ, κ, λ, μ, ν - соответствуют конечным состояниям при вариации двух параметров одновременно.
Следует отметить, что динамику дрейфа точки состояния, при регулярно-периодическом контроле прямых диагностических параметров проследить, возможно, построив траекторию движения точки состояния во времени и в двумерном пространстве прямых диагностических параметров. Сопоставив построенную траекторию точки с одним из вариантов сочетания областей изменения прямых диагностических параметров, можно сделать заключение о характере и направлении изменения контролируемых параметров СЕ. Это дает возможность обнаружить динамику изменения состояния ОД, и при длительной эксплуатации ОД периодически делать заключения о текущем состоянии ОД, а также определять характер, направление и область изменения параметров СЕ во времени, что может быть полезной информацией для составления прогноза технического состояния.
Сущность методики диагностирования состоит в определении координат точки текущего состояния в двумерном пространстве диагностических признаков посредством измерения численных значений функций передачи двух выбранных каналов диагностирования. При выполнении процедуры поиска одиночных дефектов однозначность соответствия диагностируемых параметров диагностическим признакам в обратной задаче сохраняется. Однако попытка применения рассмотренной методики к решению задачи поиска множественных дефектов приводит к нарушению однозначности соответствия. Действительно регистрируемое положение точки состояния будет являться результатом вариации параметров сразу нескольких СЕ (при возникновении множественных дефектов), приводящее к движению точки сразу по нескольким кривым в пространстве диагностирования.
Попытка решить обратную задачу, т. е. определить результатом каких элементарных перемещений и по каким кривым является ее зафиксированное (измеренное) положение приводит к неоднозначности.
Одним из направлений перехода от решения задачи поиска одиночных дефектов к решению задачи поиска множественных дефектов может быть направление, связанное с увеличением размерности пространства диагностирования и построением диагностической модели в этом пространстве. Результаты исследований теории и практики решения задачи поиска множественных дефектов в электрических цепях рассмотрены в последующих главах.