Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Применение метода исключения варьируемого параметра при решении задач диагностирования

Портнягин Н. Н., Пюкке Г. А.,

3.1. Построение диагностической модели в многомерном пространстве диагностирования

При диагностировании системы с множественными дефектами количество уравнений модели необходимо увеличить. Имеющее место в системе (2. 3) взаимно-однозначное соответствие между множеством наборов значений параметров g_i и множеством точек пространства диагностирования {K_mn ; K_kp} нарушается. Это связано с невозможностью одновременного исключения из системы более одного параметра и, как следствие, получения уравнения изовары, соответствующей вариации двух или более параметров. Одним из направлений перехода от решения задачи поиска одиночных дефектов к решению задачи поиска множественных дефектов может быть направление, связанное с увеличением размерности пространства диагностирования и построением  диагностической модели в этом пространстве.

При диагностировании методом исключения варьируемого параметра решается обратная задача, состоящая в определении координат точки текущего состояния в двумерном пространстве диагностических параметров. Однако при возникновении множественных дефектов решение задачи диагностирования  на плоскости теряет однозначность в силу того, что положение точки состояния будет являться результатом движения сразу по нескольким изоварам, и нельзя однозначно определить, результатом каких элементарных перемещений является ее зафиксированное положение, т. к. все изовары компланарны.  Восстановить однозначность решения обратной задачи можно переносом ее рассмотрения в трехмерное пространство прямых диагностических параметров, но для этого необходимо из всего множества функций передачи отобрать уже не две, а три оптимальные функции:

 K_mn = F(g₁, g₂,. . . . .. . .,g_m); 

  K_kp = F(g₁, g₂,. . . . . . . .,g_m);     (3. 1)

 K_rs  = F(g₁ , g₂,. . . . . . ., g_m).

Имея в распоряжении K_mn , K_kp , K_rs, можно зафиксировать в соответствии с номинальными значениями проводимости элементов от g₁ до g_m-1включительно и получить систему:

 K_mn = F ( g_m );

 K_kp = F  ( g_m ); 

K_rs = F  ( g_m ).

Из полученной системы попарно исключается параметр g_m и записывается система:

 K_mn = F( K_kp );

  K_kp = F( K_rs  );

  K_rs  = F( K_mn ).

Для дальнейших расчетов из трех функций достаточно взять две любые, геометрически интерпретируемые изоварой в пространстве, образованной пересечением двух ограниченных цилиндрических поверхностей с направляющими отрезками гипербол K_mn = F(K_kp )  и K_kp = F(K_rs ).

Полученная изовара является геометрическим местом точек изменения численных значений функций передачи K_mn, K_kp , K_rs при вариации исключенного параметра g_m в пределах от нуля до бесконечности. Аналогично, исключая из (3.1) последовательно параметры от g₁  до  g_m-1  включительно, получим систему некомпланарных изовар в пространстве трех измерений:

K_mn  = F₁ (K_kp );    K_mn = F₂ (K_kp );  . . . . . . .  K_mn = F_m(K_kp );   

K_kp  =  F₁ (K_rs );  K_kp  = F₂ (K_rs );  . . . . . . .  K_kp = F_m(K_rs );

Тогда поверхностью идентификации двойного дефекта будет поверхность, образованная поступательным скольжением изовары (гиперболы) β:

A K_mn²  +  BK_mn  K_rs  +  C K_rs²  +  D K_mn  +  EK_rs  =  0, по изоваре (гиперболе) α: [(K_rs – а)² / а² ]  –  K_kp²/b² = 1  в новой системе координат, где: 0 – вершина гиперболы α в плоскости K_kp0K_rs. Подсистема K_kp 0 K_rs – прямоугольная, K_mn 0 K_rs – косоугольная подсистема в плоскости гиперболы β. В силу инвариантности степени уравнения поверхности относительно преобразования координат, для произвольной точки поверхности идентификации в новой системе 0 K_kp  K_mn  K_rs можно записать:

[Cа²K_kp²/b² + АK_mn² + CK_rs² + BK_mn  K_rs+(Bа + D)K_mn + (E + 2C)K_rs + (Eа +Са²)]² = а²(1+ K_kp²/b²) (BK_mn + 2CK_rs + 2Cа + Е)². (3. 2)

После получения совокупности таких поверхностей, количество которых R определяется комбинаторно (R=C_d², где d – количество изовар), решение задачи идентификации двойного дефекта сводится к установлению принадлежности точки состояния M ^’ (Рис.3. 1) с координатами M ^’ (K_kp1 , K_mn1 , K_rs1) одной из поверхностей из данной совокупности. Для идентификации необходимо измерить три величины: K_kp1 , K_mn1 , K_rs1.

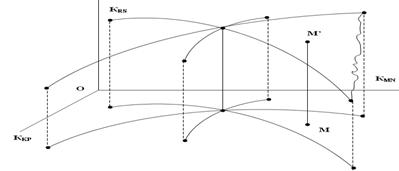
Рис. 3.1. Поверхность идентификации двойных дефектов

Проблема, случайно обнаруженной компланарности изовар, снимается заменой одного из диагностических признаков следующим по чувствительности из упорядоченного ряда прямых диагностических признаков. Численные значения коэффициентов полинома могут быть определены методом наименьших квадратов с помощью решения системы, полученной на основании полинома (3. 2) относительно неизвестных коэффициентов, при подстановке в эту систему численных значений координат точек М_i (K_kp , K_mn , K_rs),  где i = 1,…, v  , v – количество экспериментов.

Таким образом, имея такую модель ОД, можно с помощью трех измерений идентифицировать двойной дефект в сложной разветвленной электрической цепи, что существенно сокращает затраты средств и времени при диагностировании сложных систем.

При возникновении дефектов более высокого порядка однозначность решения задачи диагностирования восстанавливается увеличением размерности пространства прямых диагностических параметров. Следует отметить, что полученная модель значительно сложнее модели поиска одиночных дефектов, и ее сложность быстро возрастает с увеличением количества возможных дефектов, поэтому были исследованы другие пути решения этой проблемы, о которых говорится ниже.