Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Применение метода исключения варьируемого параметра при решении задач диагностирования

Портнягин Н. Н., Пюкке Г. А.,

3.4. Вероятностная модель диагностирования, получаемая на основе метода исключения варьируемого параметра

Применение детерминированной модели диагностирования (2.3), при решении задачи построения области работоспособности ОД, позволяет контролировать появление только одиночных дефектов. При этом необходимым условием проведения процедуры диагностирования является наличие предварительной информации о возникновении в системе только одиночных отказов. При появлении двойных, тройных и т. д. отказов область работоспособности на основе детерминированной модели (2. 3) не определена, в силу потери однозначности соответствия между множеством значений диагностируемых параметров g_i и совокупностью диагностических признаков {K_1, K₂ }. Недостатки такого рода при решении многомерных задач характерны для детерминированных моделей. Одним из способов их преодоления является введение в рассмотрение вероятностных характеристик при оценке состояния системы. Действительно, при рассмотрении различных вариантов сочетания вариаций параметров компонент в соотношениях (2. 3) количество попаданий в произвольную точку пространства диагностических признаков {K_1, K₂} зависит от положения этой точки.

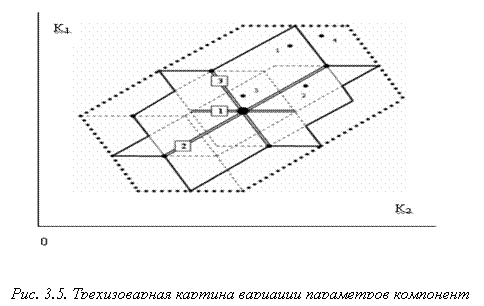
Например, для трехизоварной картины (изовары 1, 2, 3; рис. 3. 5) при заданных интервалах изменения параметров составляющих компонент g_i, i = 1, 2, 3, попадание в точку 1 можно выполнить посредством одновременной вариации второй и третьей компонент. Для попадания в точку 2 – первой и второй или второй и третьей. Для попадания в точку 3 – первой и второй или второй и третьей или первой и третьей. А для попадания в точку 4 необходима одновременная вариация уже трех компонент. Вариацией параметров трех компонент также можно переместиться в точки 1, 2, 3.

  Таким образом, для каждой точки пространства диагностирования существует свое множество конечных положений различных вариантов перемещения при вариации параметров компонент. То есть каждой точке плоскости К₁ , К₂ может быть поставлено в соответствие счетное множество векторов параметров компонент, а в поле пространства диагностирования имеет место статистическая устойчивость распределения событий. Для количественной оценки полученной закономерности необходимо посредством модели (2. 3) вычислить количество векторов параметров компонент, принадлежащих каждой точке пространства диагностирования {K_1, K₂} (рассматриваются все векторы с различной кратностью вариаций).

Введем множество G возможных реализаций численных значений компонент вектора  параметров  компонент,  где m  –  количество  двухполюсных

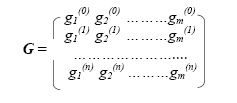
компонент эквивалентной схемы замещения; g_i – значение i – го диагностируемого параметра на интервале [0, ); n – номер реализации. Каждая строка матрицы G соответствует очередной реализации вектора параметров компонент. Введем также множество конечного числа событий А, перечисляющее все возможные состояния системы N = 2^m . Это множество состоит из конечного числа подмножеств А_j , j = 0,1,2,….,m; каждое из которых включает в себя cостояния нулевых, одиночных, двойных и т. д., m – кратных дефектов. Их количество определяется комбинаторно (С_m⁰ – количество нулевых;C_m¹ – одиночных; С_m² – двойных и т. д., С_m^m – m  – кратных дефектов). Под дефектом будем понимать выход параметра компоненты g_i за установленные пределы [g_i min , g_i max], и нарушение одного или нескольких соотношений  наблюдаемых признаков K₁, K₂

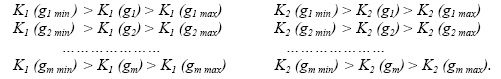
Для каждой точки пространства наблюдаемых диагностических признаков {K_1, K₂ } введем счетное множество событий В_к, определяющих количество реализаций вектора параметров компонент из генеральной совокупности G, принадлежащих данной точке (т. е. реализации вектора приводящие в данную точку). Введением множества В_к формализуется оценка многозначности функции состояния ОД при его наблюдении в пространстве диагностирования. Среди совокупности реализаций, принадлежащих данной точке, отберем подмножества  векторов соответствующих различной кратности вариаций. Тогда для каждой точки пространства диагностических признаков можно определить условную вероятность P(A_j | B_k)наступления события А_j при условии нахождения системы в выбранной точке. Так как множество В_к состоит из непересекающихся элементов, то справедлива формула полной вероятности:

P(A_j) = P(A_j ¦B_k),

где P(A_j) – вероятность наступления j – го события, удовлетворяющая следующим условиям: 0 ≤ P(A_j) ≤ 1, P(A) =  P(A_j). Таким образом, точкам плоскости К₁, К₂ может быть поставлено в соответствие конечное множество векторов состояний ОД, в которых он может находиться, и вычислены условные вероятности P₀(A₀| B_k); P₁(A₁| B_k); P₂(A₂| B_k);………..; P_m(A_m| B_k); возникновения нулевых, одиночных, двойных, и т. д., m – кратных отклонений параметров компонент в каждой точке пространства диагностирования {K₁ , K₂}. Это дает возможность каждой точке плоскости K₁ ,K₂ поставить в соответствие вектор вероятностей всех 2^m возможных состояний: Р = [Р₀ Р₁(1) P₁(2) ……..P₁(m) P₂(1) P₂(2)……..P₂(C_m²)……..P_m(1) P_m(2)……..P_m(C_m^m)] (индекс в круглых скобках обозначает номер состояния в подмножестве данной кратности; нижний индекс обозначает кратность вариации), и построить трехмерный массив калибровки пространства диагностирования  {K₁ , K₂} по вероятностям состояний различной кратности отказов (Рис. 3.6).

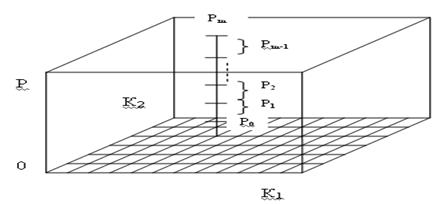
Рис. 3.6. Массив калибровки пространства диагностирования

Необходимо отметить, что количество попаданий в любую фиксированную точку пространства {K₁ , K₂} при всех сочетаниях вариаций параметрами различных компонент ОД образуют полную группу событий.  Для вектора вероятностей состояний можно написать:

P₀ +P_i^N = 1,  где R = C_mⁱ.

После калибровки необходимо решить задачу распределения в пространстве диагностирования вероятностей отказов различной кратности j, (j = 0,1,2,….,m) и определении положений их максимумов. Решить аналитически такую задачу не представляется возможным из – за трудности и громоздкости получения выражений, определяющих связь совокупности значений К₁ , К₂ с множеством всех значений параметров компонент ОД g_i . При решении таких сложных задач, как правило, применяют метод статистических испытаний. Для его реализации можно использовать современные среды прикладного программирования, такие как MATLAB, VISUAL BASIC, EXEL и др. Разрабатываемый метод позволяет оценить все функции условных вероятностей и решить основные задачи диагностирования. Действительно, по максимуму условной вероятности можно определить наиболее вероятные состояния ОД, если в каждой точке  плоскости К₁, К₂ известны значения компонент вектора условных вероятностей. Таким образом, все пространство основных диагностических признаков будет представлено совокупностью 2^m ячеек, каждой из которых можно поставить в соответствие  состояние ОД из множества допустимых состояний. Это дает возможность в вероятностной постановке решать основные задачи диагностики: поиск дефектов, определение степени работоспособности и прогнозирование технического состояния  СЭСА.