Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
Применение метода исключения варьируемого параметра при решении задач диагностирования
Портнягин Н. Н., Пюкке Г. А.,
4.3. Построение апостериорной модели деградации систем, методика, алгоритм и программа определения предотказных состояний
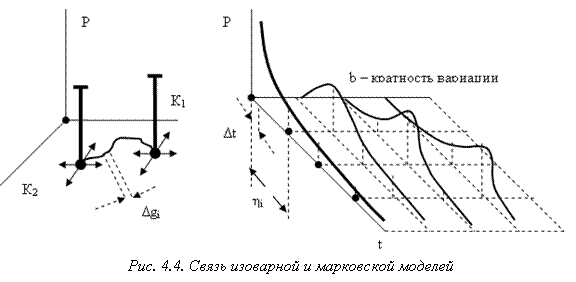
Процедура построения апостериорной модели деградации системы базируется на идее согласования динамической априорной марковской модели деградации с изоварной моделью. Марковская модель описывает развитие системы на конечном интервале времени, в пределах которого вероятностный процесс носит стационарный характер. Конечный вид изоварной модели формируется в установившемся режиме на бесконечном времени. В отличие от марковской, изоварная модель строится на основе информации о топологии конкретного объекта. Эту информацию можно использовать для адаптации вероятностного процесса деградации к диагностируемому ОД, с целью получения модели более адекватно описывающей динамический процесс старения системы (Рис. 4.4). Вектор вероятностей всех рассматриваемых состояний системы формируется посредством как марковской, так и изоварной моделей. Изоварная модель генерирует компоненты вектора в каждой точке пространства диагностирования {K1, K2}, на основе данных о топологии ОД и номинальных значений параметров компонент.
.
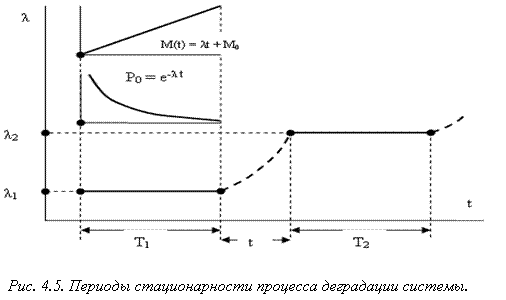
Априорная марковская модель описывает эволюцию компонент вектора вероятностей состояний системы на основе паспортных статистических характеристик надежности составляющих компонент ОД. Одной из таких характеристик является покомпонентная интенсивность отказов λ, задающая вероятности переходов стохастической матрицы РР. Однако значения λ в период эксплуатации отличаются от среднестатистических: ее величина зависит от скорости изменения параметров компонент. Вычисление именно этих λ и определит характер процесса старения системы. Для случая стационарного процесса среднее количество отказов М(t) на интервале (0,t] изменяется по линейному закону. М(t) = λt + M0 , где М(t) – математическое ожидание случайной величины отказов на интервале (0, t]. Тогда интенсивность отказов λ будет оставаться постоянной величиной
λ(t) = 
= λ
в течение всего периода стационарности Т1 или Т2 (Рис. 4.5). В период времени t нарушается линейный характер изменения математического ожиданияМ(t), процесс становится нестационарным, интенсивность отказов возрастает. Аналитическому описанию поддаются периоды стационарности, которые принимаются к рассмотрению при формировании модели. Будем выполнять односторонние вариации параметров составляющих компонент ОД gi+= var, i = 1, m, выбрав за начальные значения, номинальные значения параметров gi ном . Полагая скорости Vi изменения параметров gi постоянными, параметры меняющимися по линейному закону gi = Vi t + gi ном , а среднее время наработки на отказ ηi откз по каждой компоненте известным, выразим приращения параметров компонент Δgi через приращения, соответствующие временному шагу Δt воздействия стохастической матрицы РР на текущий вектор вероятностей состояний системы Р , получаемые при построении априорной марковской модели деградации системы.
.
.
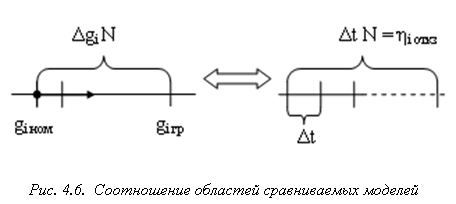
На основе физического анализа условий работоспособности ОД зададим граничные значения вариаций параметров компонент gi гр . Далее, приняв среднее время наработки на отказ ηi откз по каждой компоненте равным времени достижения параметра gi его граничных значений gi гр, можно аналитически связать величину шага Δgi с временным шагом Δt. Для доказательства, с одной стороны, на основе априорной марковской модели можно записать ηi откз = Δt N, где N – количество шагов воздействия стохастической матрицы РР, необходимое для вычисления времени наработки на отказ. С другой стороны, из изоварной модели следует следующее соотношение Δgi N = | gi ном - gi гр | (Рис. 4.6).
Приравнивая количество шагов, получим соотношение, связывающее приращения параметров и времени:
Δgi = (| gi ном - gi гр | ⁄ ηi откз ) Δt .
Обозначим | gi ном - gi гр | ⁄ ηi откз = Нi , где - Нi коэффициент пересчета величин, т.е. между моделями устанавливается соответствие, позволяющее их одновременный запуск. После задания шага изменения параметров компонент определяется величина шага времени, приводящая к согласованию моделей. Δgi= Нi Δt; Δt = Нi-1 Δgi . После согласования моделей (изоварной и априорной марковской) в рассмотрение вводится время и вычисляются изменения условных вероятностей во времени по всем 2m состояниям. Разработана программа моделирования временных зависимостей условных вероятностей по состояниям ОД, выполненная на языке VISUAL BASIC. На рис. 4.7 приведены результаты моделирования, где даны временные зависимости условных вероятностей по каждому из 64 состояний вектора условных вероятностей для шестикомпонентной эквивалентной цепи схемы мостового выпрямителя.
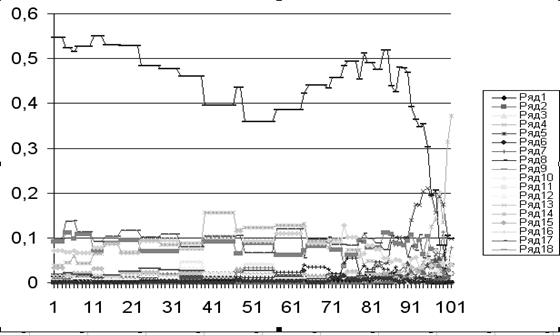
Рис 4.7. Временные зависимости условных вероятностей по состояниям работоспособности и кратных отказов мостового выпрямителя
На рис. 4.8. приведена трехмерная экранная форма процедуры моделирования, где выведены 18 выборок состояний из 64 смоделированных, каждая из которых развернута на интервале 101 шагов дискретного времени. При одновременном запуске моделей в момент t = 0 (для марковской модели) и при начальных значениях параметров компонент gi = gi ном (для изоварной модели) с последующим нарастанием количества шагов N, точка состояния перемещается по результирующей траектории в пространстве диагностических признаков {K1, K2}. Параметр i – й компоненты приближается к своему граничному значению gi гр и в момент выхода за допустимые пределы, согласно установленной связи с марковской априорной моделью деградации, вероятность отказа соответствующей компоненты достигнет максимума (Рис. 4.9.). Так как пространство диагностирования откалибровано и в каждой точке (дискретной ячейке) плоскости K1, K2 известен вектор условных вероятностей всех состояний, то можно пересчитать все компоненты вектора вероятностей для марковской модели.
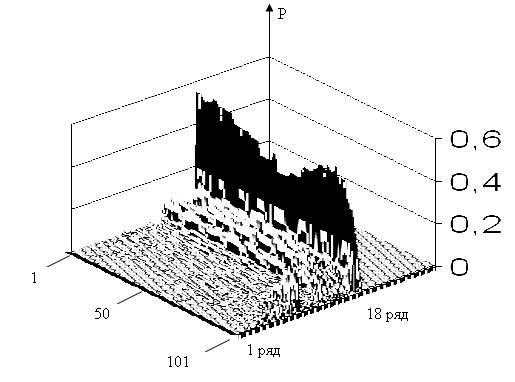
Рис. 4.8. Экранная форма результата моделирования выборок состояний мостового выпрямителя
Пересчет будем выполнять в точках кратных найденному значению Δt.
Рис. 4.9. Изоварная (а) и марковская (б) модели
В пределах периода стационарности процесса, при вариациях параметров составляющих компонент gi интенсивность λ отказов остается величиной постоянной. Вычисление апостериорных вероятностей выполняется по каждой компоненте вектора вероятностей состояний Рj , j = 0, 1,….,2m и для варианта сочетания вариаций параметров всех компонент gi ОД. Выполнение одновременных вариаций параметрами всех gi компонент продиктовано условием постепенного изменения параметров всех составляющих компонент во времени при описании процесса деградации марковским случайным процессом. Все условные вероятности вычисляются по формуле переоценки гипотез. Обоснованием использования бейесовской теоремы гипотез является следующее умозаключение: текущий вектор вероятностей состояний Р = [Р0 Р1(1) P1(2)……..P1(m) P2(1) P2(2)…..P2(Cm2)……..Pm(1) Pm(2)……..Pm(Cmm)], порождаемый марковской моделью в моменты времени k ?t, при k = 0, 1, 2,……, является вектором априорных вероятностей появления в системе отказов различной кратности или их отсутствия. Эта информация отражает общие тенденции деградации и слабо связана с изучаемым ОД (только через λ). Так как информация, поступающая от марковской модели базируется на статистических данных о показателях надежности составляющих компонент ОД, то численные значения компонент вектора вероятностей состояний системы можно рассматривать как вероятности гипотез В1, В2,…., Вn , выдвинутых до проведения измерения, выполненных посредством изоварной модели. Т. е. априорные вероятности гипотез заданы, образуют полную группу событий и равны: Р(В1), Р(В2),…., Р(Вn); 
P(Bi) = 1. После проведения опыта на изоварной модели необходимо пересмотреть вероятности гипотез Р(В1), Р(В2),…., Р(Вn) с учетем информации полученной от изоварной модели. Другими словами, необходимо найти апостериорные вероятности гипотез появления кратных отказов или их отсутствия, при условии, что в результате измерения на изоварной модели появилось событие А, состоящее в регистрации отказа той или иной кратности: РА (В1), РА(В2),…., РА(Вn). При этом, вектор РВi(А)условных вероятностей наступления события А при выполнении гипотез Bi уже известен при измерениях на изоварной модели. Вероятности вычисляются для каждой компоненты вектора вероятностей состояний (4. 1). В результате становятся известными компоненты вектора апостериорных вероятностей.
.
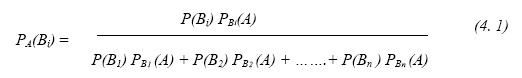Следует отметить, что для непосредственного применения соотношения (4. 1) сначала необходимо ввести соотношения синхронизации, позволяющие при каждом акте вычисления выбирать таутахронные (синхронизированные по времени при согласовании моделей) пары векторов вероятностей от марковской и изоварной моделей. Задачу можно реализовать нахождением аналитической связи между варьируемыми параметрами компонент Δgi , приращением времени Δt и численными значениями диагностических признаков К1 и К2 .
.
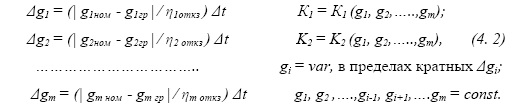Процесс синхронизации задает программа “Nakoplenie 1”, выполняющая перебор всех вариаций параметров компонент gi , с шагом Δgi . Программа выбирает все те сочетания вариаций параметров компонент различной кратности, которые приводят в выбранную точку пространства диагностирования {K1, K2}, вектор условных вероятностей в которой уже известен (в результате операции калибровки пространства). Аналитически эта операция будет сводиться к проверке выполнения соотношений (4. 2) и нахождению координат (K1, K2) вектора вероятностей состояний, при различных сочетаниях вариаций параметрами компонент ОД по заданному шагу изменения времени Δt. После нахождения таутахронных векторов возможно непосредственно воспользоваться соотношением (4. 1) для нахождения апостериорных вероятностей. Запишем соотношение (4. 1) для случая условных и априорных вероятностей, определяемых изоварной и марковской моделями соответственно.
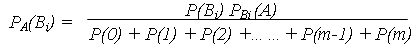
где Р(0) = Р(В0) РВ0 (А);
Р(1) = Р(В11) РВ11 (А) + Р(В12) РВ12 (А) +…….+ Р(В1m) PB1m (A);
P(2) = P(B21) PB21 (A) + P(B22) PB22 (A) +…….+ P(B2K) PB2K (A);
…………………………………………………………………………
P(m-1) = P(Bm-1,1)PB m-1,1(A) + P(Bm-1,2)PB m-1,2(A) +……+ P(Bm-1,R)PB m-1,R(A);
P(m) = P(Bm)PBm(A).
K = Cm2; ……;R = Cmm-1 – комбинаторные сочетания – числа определяющие количество слагаемых в выражении (4.3) по вариациям различной кратности.
P(Bi) – вероятность наступления одной из вариаций i – й кратности,
i = 0, 1, …, m;
PBi (A) – условная вероятность попадания в точку с координатами (К1, К2), при разыгрывании случайной величины параметра компонент ОД, при условии выполнения одной из вариаций i – й кратности.
А – событие, состоящее в том что текущее состояние принадлежит точке с координатами (К1, К2).
Bi – событие, состоящее в наступлении одной из вариаций i – й кратности.
В0, В11, В12,……, Вm – образуют полную группу событий.
PA(Bi) – апостериорная условная вероятность того, что текущее состояние, соответствующее одной из вариаций i – й кратности принадлежит точке с координатами (К1, К2).
.
Процесс синхронизации моделей включает два этапа: 1. Нахождение таутахронных векторов вероятностей состояний. 2. Вычисление компонент вектора апостериорных вероятностей. Первый этап начинается с задания интервала времени Δt, известного из построения априорной марковской модели и нахождении всех Δgi по полученным соотношениям.
Исходной задающей величиной процесса деградации системы (при одновременном описании марковской и изоварной моделью) является скорость вариации Vi параметров составляющих компонент gi . Если предположить, что скорости вариации параметров отдельно взятых компонент постоянны, то можно записать систему линейных соотношений, описывающих характер изменения параметров составляющих компонент в процессе эксплуатации ОД.
gi = Vi t + gi ном ; (4. 4)
где i = 1, m; gi ном – номинальные значения параметров компонент.
Системе (4.4) будет соответствовать совокупность графиков (Рис. 4.10), где обозначены граничные значения параметров gi гр и моменты наступления отказов составляющих компонент ОД ti отк .
С другой стороны, для отдельно взятой партии компонент данного назначения, используя количественные показатели надежности, можно ввести величину математического ожидания как одну из характеристик случайного процесса деградации параметров компонент, для достаточно большой совокупности одинаковых элементов. На рис. 4.11. обозначены граничные значения параметров gi гр и величины среднего времени наработки на отказ ηiоткз. Исключая из рассмотрения производственный разброс параметров компонент на исходные значения gi ном (определяемые в основном условиями производства элементной базы), введем в рассмотрение случайную величину скорости изменения параметров составляющих компонент Vi, разброс численного значения которой будет определяться в основном условиями эксплуатации.
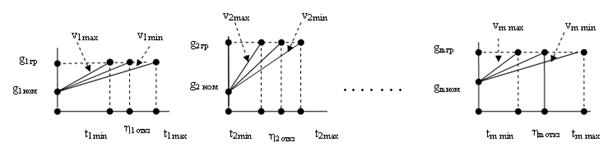
Рис. 4.11. Граничные значения параметров компонент
Полагая случайную величину скорости Vi распределенной по нормальному закону и используя метод статистических испытаний, можно определить параметры нормального закона распределения (математическое ожидание и среднеквадратическое отклонение) после разыгрывания случайной величины скорости Vi . Это дает возможность выразить плотность вероятности случайной величины времени ft (t) через плотность вероятности случайной величины скорости fv (v), используя соотношения gi = Vi t + gi ном , и при условии, что в пределах [Vi min , Vi max] функция gi = Vi t + gi номмонотонна. На основании сказанного можно записать
ft (t) = fv (|gi – gi ном| ⁄ t) |d(|gi – gi ном| ⁄ t) ⁄ dt|.
Решая совместно системы
gi = Vi min t + gi ном ; gi = Vi max t + gi ном ;
gi = gi гр ,
получим границы изменения времени
ti min = (gi гр – gi ном) ⁄ Vi max ;
ti max = (gi гр – gi ном) ⁄ Vi min .
После нахождения обратной функции Vi = |gi – gi ном| ⁄ t и ее производной dVi ⁄ dt = - |gi – gi ном| ⁄ t2 можно определить закон распределения случайной величины времени ft (t). Связь между скоростью вариации параметров компонент, среднем временем наработки на отказ и интенсивностью отказов следует из соотношений:
Vi = ?gi ⁄ ?t = | gi гр – gi ном | ⁄ ηi откз = | gi гр – gi ном | λi .
Можно показать, что время достижения граничных значений варьируемым параметром, при использовании соотношений связи моделей равно среднему времени наработки на отказ по каждой компоненте:
gi – gi ном = Vi t; t = (gi – gi ном) ⁄ Vi ; Vi = | gi гр – gi ном | ⁄ ηi откз ;
t = [(gi – gi ном) ⁄ ( gi гр – gi ном )] ηi откз , тогда при gi = gi гр получим t = ηi откз .
Используя полученные соотношение можно определить необходимые скорости изменения параметров компонент ОД, обеспечивающие достижение граничных значений (на основе изоварной модели) и среднего времени наработки на отказ (при рассмотрении марковской модели).
Согласование статистической информации по показателям надежности компонент ОД, реализуемую через априорную марковскую модель деградации, с информацией о характере и свойствах конкретного ОД можно выполнить посредством регулирования параметра ηi откз в уравнениях связи, при согласовании компонент вектора апостериорных вероятностей PA(Bi) с компонентами вектора априорных вероятностей. Задача сводится к выбору такой скорости изменения параметров компонент и связанной с ней интенсивностью отказов и среднем временем наработки на отказ, которые обеспечат согласование компонент векторов апостериорных и априорных вероятностей.
Коррекцию численных значений величин интенсивностей отказов λi можно выполнить посредством минимизации функционала расхождения векторов апостериорных и априорных вероятностей состояний системы во времени
| Рапостер i (k ?t; λ) – Pаприор i (k ?t; λ) | -> min.
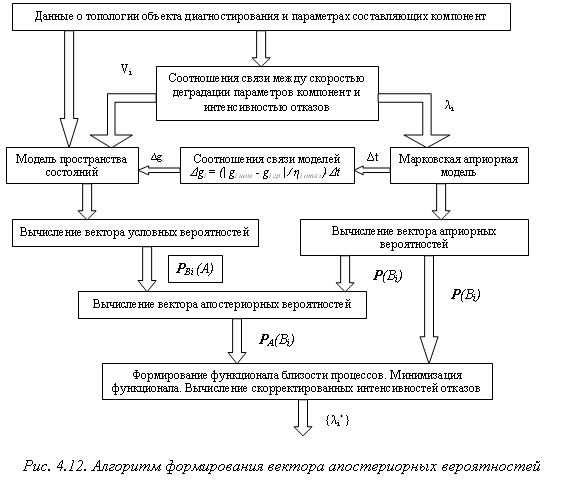
На рисунке 4.12 приведен алгоритм формирования вектора апостериорных вероятностей состояний системы, описывающей динамический процесс старения системы. Вектор строится на основе информации получаемой от конкретного объекта диагностирования, при использовании модели пространства состояния (изоварная модель) для построения вектора условных вероятностей состояний системы. С другой стороны задается вектор априорных вероятностей состояний системы, построенный на основе марковской модели и отражающий общие тенденции развития систем, с использованием статистических данных о показателях надежности составляющих компонент, рассматриваемой системы.
.
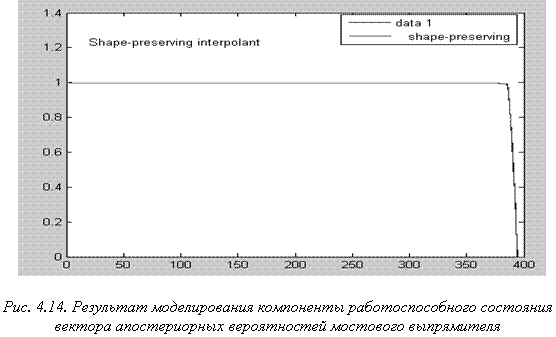
Использование соотношений связи моделей дает возможность синхронизировать процесс и вычислить компоненты вектора апостериорных вероятностей, дать объективную оценку расхождения процессов и вычислить значения интенсивностей отказов, соответствующие минимуму функционала близости. Ниже приведена программа построения графика временной зависитмости компоненты работоспособного состояния вектора апостериорных вероятностей состояний ОД. На рис. 4.14. приведен результат выполнения программы для шестикомпонентной схемы мостового выпрямителя. Как следует из графика, в результате корректировки модели на основании топологических данных ОД, характер поведения вероятности работоспособного состояния ОД изменился. Закон изменения вероятности работоспособного
.
состояния ОД, как следовало ожидать, уже не носит экспоненциального характера. Компонента работоспособности вектора апостериорных вероятностей сохраняет численное значение равное 1 до момента появления единичного или кратных отказов.
.
Это свидетельствует о том, что информация о конкретном ОД, полученная посредством изоварной модели, скорректировала общий характер деградации системы, определяемый марковским процессом старения. Таким образом, наступления предотказного состояния ОД может быть прогнозировано по вычисленному времени наработки до отказа по быстрому уменьшению вероятности работоспособности в определенный момент времени.