Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Применение метода исключения варьируемого параметра при решении задач диагностирования

Портнягин Н. Н., Пюкке Г. А.,

2.2.1. Формирование массива коэффициентов передачи при анализе объекта диагностирования

Учитывая особенность средств ЭКТ как объекта диагностирования и характер решаемых задач в качестве совокупности основных диагностических признаков выбирается множество функций передачи электрической цепи. Диагностируемая электрическая  схема или ее часть представляется в виде совокупности структурных единиц, размер которых определяется глубиной диагностирования. При таком делении электрической цепи диагностирование ведется с точностью до структурной единицы, а весь ОД представляется как n – полюсная система (Рис. 2. 2).  Исходным из всех состояний ОД будет считаться состояние S₀, соответствующее совокупности номинальных значений диагностируемых параметровg_iном. Всякое отклонение параметра g_i произвольной СЕ или совокупности СЕ от номинального значения считается новым состоянием S_i , принадлежащим области работоспособных или неработоспособных состояний. Тогда каждому состоянию S_i ставится в соответствие определенная совокупность значений диагностических  признаков  {K_j}. Область  работоспособности  определяется как область изменения диагностических признаков, в границах которой ОД работоспособен, а значения g_i находятся в области допустимых значений. Согласно рассмотренной методике поиска дефектов и определения степени работоспособности ОД осуществляется путем контроля упорядоченного и минимизированного множества основных диагностических признаков,  порождаемых исходной матрицей узловых проводимостей цепи, представленной в виде многополюсной системы, либо с помощью сигнального или топологического графа, теоремы Мезона и т. д.

 .

 .

Для формализации решения поставленной задачи используется аппарат матричных преобразований. Формирование множества основных диагностических признаков начинается с построения полной или укороченной матрицы узловых проводимостей G^(у) диагностируемого фрагмента электрической схемы. При машинной обработке информации удобно использовать соотношение: G^(у) = А G^(в) A^t. Матрица G^(у) формируется вводом в ячейки памяти матриц А и G^(в) , где А – матрица инциденций, G^(в) – диагональная матрица проводимостей ветвей. С этой целью нами разработана программа построения модели диагностирования и графический интерфейс введения данных для формирования топологических матриц по заданному топологическому графу. На основе полученной матрицы G^(у) формируется множество основных диагностических признаков М, в качестве которых рассматриваются двумерные массивы коэффициентов передачи электрических сигналов, где Z - матрица входных и взаимных сопротивлений

K^(u) = - ZG^(в) ;

G = G^(в) K^(u) + G^(в) ;

K⁽ⁱ⁾ = G^(в)Z - 1^(в);

Z = A^t [G^(у)]^-1A;

ветвей; K^(u) – матрица массива распределения источников ЭДС; K⁽ⁱ⁾ – матрица массива коэффициентов распределения источников тока; G – матрица входных и взаимных проводимостей ветвей; 1^(в) – единичная матрица. Матрица G^(у) является М – матрицей, т. е. имеет знакоположительную обратную  матрицу Z^(у) = [G^(у)]^-1. Матрица Z^(у) – симметричная для взаимных цепей матрица входных и взаимных сопротивлений ветвей инцидентных опорному полюсу.

Мощность множества М определяется комбинаторно и для безразмерных функций цепи K^(u) и K⁽ⁱ⁾ составляет: М_u = M_i = (C_n² – 1)C_n², где n – количество

полюсов многополюсной системы. Для размерных функций цепи Z и G мощность множества составляет: М_u = M_i = 0, 5 (C_n² – 1)C_n² . МножествоМ основных диагностических признаков подразделяется на подмножества М₁, М₂ , М₃ по признаку инцидентности опорному полюсу. Такая градация необходима для получения общих выражений, формирующих множество миноров для подсчета коэффициентов передачи массивов Z K^(u) K⁽ⁱ⁾ Gразличных информативных каналов диагностирования. Здесь М₁ = 2 С_{n – 1}² – количество функций передачи {K_s-k } как по входу s так и по выходу k инцидентных опорному полюсу; М₂ = C_{n – 1}²(C_{n – 1}² –  1) – количество  функций передачи {K_lm-kf }как по входу lm, так и по выходу kf неинцидентных опорному полюсу; М₃ = 2(n – 1)C_{n – 1}² – количество функций передачи {K_{s – lm}  } инцидентных по входу s и неинцидентных по выходу lm нулевому полюсу. Справедливость комбинаторных соотношений можно показать: М = М₁ + М₂ + М₃ = 2С_{n – 1}² + C_{n – 1}² (C_{n – 1}² – 1 ) + 2(n – 1)C_{n – 1}² =  (n – 1)(n – 2) + [((n – 1)(n– 2) / 2 )((n – 1)(n – 2) / 2) – 1)] + (n – 1)(n – 2)(n – 1) = (n⁴ – 2n³ – n² + 2n) / 4 = (n⁴ – 2n³ + n² – 2n² + 2n) / 4 = [(n² (n² – 2n + 1) –2n (n– 1)] / 4 = [n (n – 1) / 2][n (n – 1) / 2] – n (n – 1) / 2 = C_n² C_n² – C_n² = C_n² (C_n²– 1) = М , что и требовалось доказать.

Для формирования всего массива функций передачи, порождаемых многополюсной системой ОД, имеют место общие соотношения, устанавливающие последовательность присвоения численных значений индексам функций передачи каналов прохождения тестового сигнала:

s = 1, 2 , ………, ( n – 2 ); k = (s + 1), ( s + 2 ), ………., ( n – 1) или k = 1, 2, ……….., ( n – 2 ); s = ( k + 1 ), ( k + 2 ), ………….,.( n – 1 ) . f = 1, 2, ………..……,( n – 3 ); g = ( f + 1), (f + 2 ), ………..( n – 2 ); l = 1, 2, ………, (n – 3); m = ( g + 1 ), ( g + 2 ),…………., ( n – 1 ). f = 1, 2, …………,( n – 3 );  g = ( f + 1 ), (f + 2 ), ……….., ( n – 1 ); l = (f + 1 ), ( f + 2 ), ……….., (n – 2 );  m = ( l + 1 ), ( l + 2 ), ……….., (n – 1).

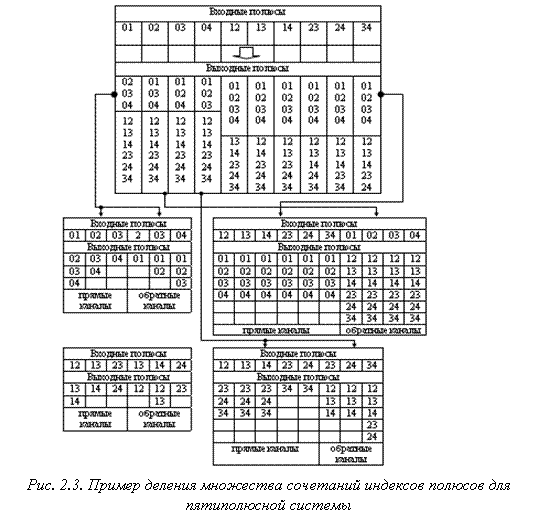
На рис. 2.3 приведен пример деления множества сочетаний индексов входных и выходных полюсов М на подмножества М₁, М₂, М₃ для пятиполюсной системы. При машинной обработке данных, массив функций передачи формируется включением четырехразрядного счетчика индексов с использованием в качестве исходной полной матрицы узловых проводимостей. Рассматривается алфавит, содержащий n  символов, где n – количество полюсов многополюсной системы. Количество всех возможных четырехразрядных кодов, составленных из n  символов М =  n⁴формируется прямым перебором с использованием кодирования индексов с помощью системы

вложенных циклов, что освобождает от резервирования больших объемов памяти. Отбор функций передачи производится вводом условий: i ‹ j;  k ‹ f;  i ≠ k;  j ≠ f, где i, j – номера полюсов подачи тестового сигнала; k,f – номера полюсов снятия информации.

.

При анализе схем средств ЭКТ, представляющих электрические цепи более высокой размерности, удобно получать функции передачи с помощью аппарата структурных чисел [8]. Кроме того, для нахождения всей совокупности функций передачи многополюсной системы используется сигнальный граф.  Рассматривая различные сочетания входных и выходных полюсов, можно получить всю совокупность функций передачи, порождаемых исследуемой цепью, представленной многополюсной системой. Для формирования множества основных диагностических признаков могут быть использованы выше приведенные способы. Далее рассмотрим методику построения массива диагностических признаков машинными методами, позволяющей автоматизировать процедуру построения совокупности функций передачи.