Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Применение метода исключения варьируемого параметра при решении задач диагностирования

Портнягин Н. Н., Пюкке Г. А.,

2.2.2. Алгоритмические методы построения совокупности знакопостоянных диагностических признаков

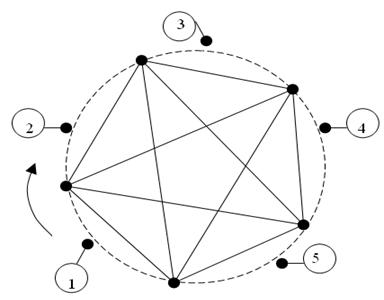
При диагностировании методом исключения варьируемого параметра в процессе измерения диагностических признаков иногда необходимо обеспечить знаковую однозначность результатов измерения численных значений функций передачи. Возможная неоднозначность имеет место в следствии перемены знака некоторых функций передачи при вариациях параметров диагностируемой системы. Если произвести отбор основных диагностических признаков по критерию знакопостоянства функций передачи, то все пространство диагностирования (основных диагностических признаков) будет принадлежать одному квадранту системы координат и однозначность идентификации по знаку будет гарантирована. Для машинного отбора знакопостоянных функций передачи разработана процедура ротации топологического графа, базирующаяся на изоморфном представлении графа диагностируемой электрической цепи произвольной размерности, представленной многоугольником с диагоналями. Это дает возможность построить подмножество N₁ функций передачи каналов инцидентных по входу и выходу любому полюсу  и обеспечить знаковую однозначность при диагностировании. Для отбора подмножества N₁ предварительно построенный  граф электрической цепи подвергается ротации: поворотом относительно неподвижных  вершин-узлов дискретно с шагом в одну дугу, начиная с позиции нулевой ротации (Рис. 2.4 ).

Записывается полная матрица узловых проводимостей G^(у) для позиции нулевой ротации, которая в дальнейшем совершает транспозиции строк и столбцов при каждом очередном дискретном повороте графа. При такой ротации происходит перераспределение потенциалов всех узлов многополюсника относительно опорного узла вследствие подключения к неподвижным узлам - вершинам различных сочетаний ветвей.

.

Рис. 2.4. Ротация графа пятиполюсной системы

Совокупность сочетаний входных и выходных полюсов каналов прохождения сигналов при ротации не изменяется. Это дает возможность каждый раз при очередном повороте графа использовать одно и то же сочетание индексов при вычислении множества миноров определителя матрицы узловых проводимостей и одно и то же соотношение для вычисления всего подмножества функций передачи N₁: К_os-ok  =  Δ _s k / Δ _s s , где К_os-ok – функция передачи от s - го входа к k - му выходу; D_sk - минор, полученный из определителя матрицы узловых проводимостей вычеркиванием s - й строки и k-го столбца; D _{s s} – соответственно s  - й строки и s – го столбца. Процессом формирования подмножества N₁ управляет квадратная матрица транспозиций индексов Т порядка n, первая строка которой соответствует нулевой ротации и определяет перестановку индексов. Каждая последующая строка получается в результате (n - 1) - транспозиций индексов предидущей строки и соответствует очередной ротации:

 Т =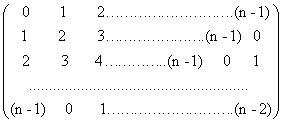 

Первый столбец матрицы Т – столбец  опорных узлов. Далее формируется вектор перебора индексов R = (1 2……….(n-1)), на основе которого строится кососимметричная матрица перебора индексов I, которая задает порядок формирования подмножества миноров D _{s k} и D _{s s} при каждой очередной ротации графа и матрицы узловых проводимостей.  Для обеспечения линейной независимости системы при каждой очередной ротации из матрицы G^(у) вычеркивается нулевая строка и нулевой столбец (с восстановлением  предшествующей структуры матрицы после каждого очередного вращения). Соответственно, нулевой индекс в вектор R не включается. Результатом (n - 1) вращений графа является деление множества

 I = 

N₁ на n подмножеств функций передачи, каждое из которых определяет совокупность функций передачи каналов, инцидентных одному из узлов – вершин  графа. После совершения полного цикла (n – вращений) система возвращается в исходное состояние. Для получения (n - 1) остальных подмножеств функций передачи необходимо произвести дешифровку индексов функций передачи для всех положений графа, начиная с первой по (n - 1) ротации. Для этого используется матрица транспозиций индексов Т. Матрица транспозиций индексов может быть представлена совокупностью последовательных отображений множества {0, 1, 2,………,(n-1)} на себя, как совокупность различных записей одной и той же подстановки n - й степени, так как каждая последующая строка матрицы Т получается отображением предидущей строки по одному и тому же закону соответствия. Это дает возможность при дешифровке индексов каждой очередной ротации применять одну и ту же подстановку А: и  обращаться  к  ней  при  каждой

А = 

очередной ротации для получения массива сочетаний индексов функций передачи всего подмножества N₁.

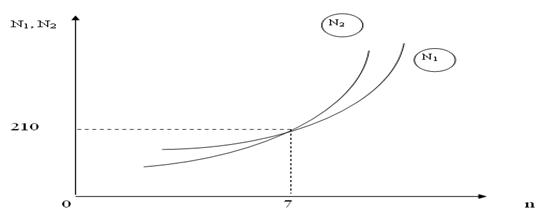
Рис. 2.5. Графики роста количества трехполюсных и  четырехполюсных каналов 

Отбор основных диагностических признаков методом вращения графа позволяет сократить объем вычислений, объем резервирования памяти, устранить неоднозначность при диагностировании методом исключения

варьируемого параметра, сократить количество полюсов съема информации. Отобранное ротационным методом подмножество знакопостоянных функций передачи N₁ характеризует совокупность трехполюсных каналов. Другое подмножество N₂ функций передачи представляет собой совокупность четырехполюсных каналов, которые могут изменять свой знак при вариациях диагностических параметров. Количество N₁трехполюсных каналов определяется комбинаторно: N₁ = n А²_n-1, где n – количество полюсов многополюсной системы. Соответственно: N₂ = C ² _n  C²_n-2 ; n ≥ 4, при n < 4 подмножество N₂ пусто.  При возрастании n размерности диагностируемой цепи количество трехполюсных каналов N₁нелинейно возрастает (Рис. 2. 5). Скорость роста количества четырехполюсных каналов N₂ выше, чем N₁. При малых n <  7 N₁ > N₂;  при n >  7 N₁< N₂, т.е. существует точка пересечения зависимостей N₁ = F(n)  и N₂ = F(n). Равенство N₁ = N₂  наступает при n = 7. Для построения диагностической модели используется пара каналов, каждый из которых имеет функцию передачи, принадлежащую одному из подмножеств N₁ или N₂. Имеют место различные комбинации попарных сочетаний каналов: 1. Оба канала четырехполюсные. 2. Оба канала трехполюсные. 3. Первый канал трехполюсный, второй четырехполюсный.

Различные сочетания пар каналов определяют характер расположения изоварной картины. Так, проведенные исследования показали, что использование сочетаний каналов первого варианта порождает семейство изовар, в общем случае, принадлежащее всем четырем квадрантам прямоугольной системы координат, использование второго варианта сочетания каналов дает изоварную систему, расположенную только в одном из квадрантов, соответственно, третий вариант порождает систему изовар, расположенную в двух смежных квадрантах. После формирования массива основных диагностических признаков, рассмотренными методами, необходимо получить их аналитические выражения.