Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

ПРОГРАММИРОВАНИЕ, УПРАВЛЕНИЕ И ЦИФРОВЫЕ МОДЕЛИ ЗАБОЕВ ГАЗОУГОЛЬНЫХ ШАХТ

Жетесова Г. С., Бейсембаев К. М., Нокина Ж. Н., Телиман И. В.,

1.3.2. Принципы макро и микромоделирования и основные уравнения движения макромоделирования

В настоящее время горные машины образуют машино-технологические системы МТС по обработке и транспортированию полезного ископаемого, чаще всего на режимы работы машин существенно влияет их взаимодействие между собой и рабочей средой. Так состояние боковых пород особенно в современных лавах существенно определяется режимом поддержания кровли механизированной крепью. От этого зависит и отжим угля (трещиноватость пласта в зоне работы комбайна), а значит и параметры отбойки. Поэтому можно говорить о расчете параметров МТС. Проектирование и конструирование МТС опирается на методы анализа НДС и динамики взаимодействия её составляющих между собой и рабочей средой. Методы расчёта НДС с учётом сложности структуры, форм машин, узлов, деталей и рабочих сред в настоящее время опираются на конечно элементные технологии, входящие в общие и специализированные программные пакеты Ansys, Nastran и частично в Adams. Последний в существенно большей степени предназначен для решения задач динамики машин на основе линеаризации их уравнений. Огромный вклад в развитие методов проектирования машин вложил Академик АН СССР, герой социалистического труда, обладатель международной золотой медали имени Дж. Уатта инженеров-механиков (Англия, 1967) Иван Иванович Артоболевский (1905–1977) сын известного ученого-богослова и протоирея Ивана Алексеевича (1872–1938). Его книга «Теория механизмов и машин» стала практическим воплощением наработанной зарубежными и отечественными учеными теории, которая составила основу проектирования машин начиная от 40-х годов 20 века. Так для расчёта первых в мировой горной практике отечественных механизированных крепей ОМКТ, МК, ОКП, ОКП-70, 3МК с четырёхзвенником Чебышева (лемнискатным механизмом) ставших прообразом современных западных систем типа Glinik был использован графоаналитический метод, основанный на построении планов скоростей и ускорения для отдельных положений механизмов. В принятой методологии систем автоматизированного проектирования расчёт нагрузок между взаимодействуюшими, движушимися деталями или узлами рассматривают как макромоделирование, где в ряде случаев необходимо учитывать силы инерции. По И.И. Артобалевскому все силы инерции звена совершающего плоскопараллельного движения и имеющего плоскость симметрии параллельную плоскости движения могут быть сведены к силе инерции Fi приложенной в центре масс S звена, и к паре сил инерции, момент которой равен mi, рис. 3.1

Fi = –m∙as, (1.5)

где Fi – вектор силы инерции; m – масса звена; аs – вектор полного ускорения центра масс S.

Вектор aS удобно определять из построенного плана ускорений, применяя свойство подобия. Момент i направлен противоположно угловому ускорению ε

mi = –Js∙ε, (1.6)

где Js – момент инерции звена относительно оси, проходящей через S и перпендикулярной плоскости движения звена.

Величину ε определим так:

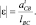(1.7)

Работа современной МТС не мыслима без контрольно регистрирующей и управляющей аппаратуры. Это накладывает требования и к кинематике работы, уровням и диапазонам допустимых нагрузок. Сказанное обуславливает единство методов и расчетов силовых и прочностных параметров такой системы на основе комплекса типовых приемов автопроектирования и программирования в специально создаваемых для системы информационных средствах. Построенные по вышеприведенным принципам системы далее были воплощены в компьютерные приложения. Так для расчёта геометрических параметров рычажных механизмов, наряду с применением пакета Adams, была разработана система распознавания области существования рычажных четырехзвенников. В ней в таблицах Excel с помощью VBA осуществляется фильтрация данных, фиксирующая в строках положения механизма с последующей графической визуализацией траекторий, в котором геометрическую оптимизацию данных проводить нагляднее и быстрее, чем в Adams. После чего данные передаются в основной пакет для продолжения проектирования.

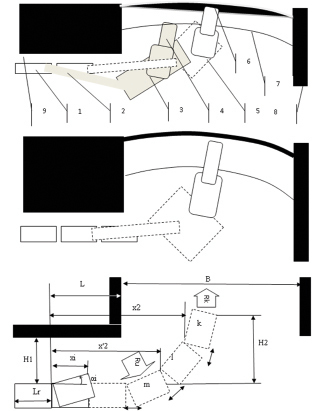
Рис. 1.9. Маневрирование конвейера:внедрение комбайна (а): 1 – конвейер; 2 – перегрузчик; 3 – комбайн; 4 – исполнительный орган; 5 – положение при маневрировании; 6, 7 – положения забоя; 8 – стенка камеры; перед поворотом конвейера (б); поворот конвейера (в)

Как известно теоретические основы программного пакета Adams базируются на основных теоремах динамики движения твердого тела. Мы остановимся на некоторых определениях, которые используются в пакете. Уравнениями Лагранжа второго рода называют дифференциальные уравнения движения механической системы, получаемые при применении лагранжева формализма (Лагранжиан представляет собой разность кинетической и потенциальной энергий системы).

Если голономная механическая система (налагающая ограничения только на положения или перемещения точек и тел системы) описывается лагранжианом 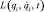(qi — обобщённые координаты, t — время, точкой обозначено дифференцирование по времени) и в системе действуют только потенциальные силы, то уравнения Лагранжа второго рода имеют вид:

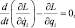(1.8)

где i = 1, 2, …, n (n — число степеней свободы механической системы).

Если в системе действуют непотенциальные силы (например, силы трения), уравнения Лагранжа второго рода имеют вид:

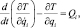(1.9)

Уравнения Лагранжа в механике получаются из законов динамики Эйлера (баланса количества движения и момента количества движения) при определенных ограничениях на систему (в ней должны присутствовать лишь идеальные голономные связи). Для других случаев получаются модификации уравнений Лагранжа. Отметим, что это частный (хотя и очень важный) случай механических систем.

Решения уравнений Лагранжа второго рода для частных случаев служат примером тестирования результатов получаемых в пакете Adams. Но в тоже время в данном учебнике предусматривается проверка полученных результатов на основе частных авторских решений.

Напряженное состояние деталей или массива, микромоделирование (рабочих средств) в зависимости от рассматриваемой геометрии, вида нагрузки и свойств материала описывается дифференциальными уравнениями, которые могут быть получены из общего квазигармонического уравнения

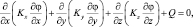(1.10)

Уравнения имеют множество решений, поэтому для выбора необходимого следует задать начальные условия. Дифференциальное уравнение в частных производных с граничными и начальными (краевыми) условиями называют дифференциальной краевой задачей или математической моделью объекта.
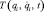