
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания

ПРОГРАММИРОВАНИЕ, УПРАВЛЕНИЕ И ЦИФРОВЫЕ МОДЕЛИ ЗАБОЕВ ГАЗОУГОЛЬНЫХ ШАХТ
Жетесова Г. С., Бейсембаев К. М., Нокина Ж. Н., Телиман И. В.,
2.2.3. Программно-управляемые манипуляторы на шахтах РК
Авто манипуляторы используются для установки анкерной и переносной крепи, зачистке кровли и почвы у сопряжений лав с выработками. Для повышения эффективности их работы необходимо совершенствование программного обеспечения при работе в режиме обратной связи. Гарантией работоспособности является наличие взаимозаменяемых программных моделей на основе типовых средств, которые обычно созданы на основе «закрытого» программного обеспечения (ПО), особенности использования которого известны не полностью. Поэтому необходимо наличие авторских средств для тестирования затруднительных и аварийных ситуаций и контроля основного ПО. Конструктивные схемы манипуляторов в основном состоят из двух – трех рычагов (рис. 2.8), а также более сложных конструкций с четырехзвенными механизмами Чебышева (см. а.с. SU 1308767, Е 21 D 23/00б 23/06). Манипулятор закреплен в точке В и переносит груз Ру, гидроцилиндр поворачивает рычаг АВ, а гидроцилиндр между точками М и N, выполняет дополнительную корректировку траектории. Для удержания от смещения штоков при неравномерных нагрузках в системе применяются гидрозамки. Расчет манипуляторов основан на составлении уравнений равновесия в сочлененных узлах с использованием тригонометрии. Для двух рычажных систем они просты, а при большем количестве рычагов применяются численные методы. Решение этих схем с линейной дискретизаций уравнений выполнено в пакете Adams в 3d. В соответствии с требованиями расчета сложных систем необходима дополнительная (обычно авторская) система тестирования. Схема на рис. 2.9 универсальна и с частными коррективами используется во многих машинах. Такая методика учитывает графо-аналитический метод Артоболевского с реализацией в табличных процессорах, которые могут создаваться средствами объектно-ориентированных языков программирования (С++, VB) или в Excel [48], что обеспечивает создание быстро исполняемых файлов типа .exe в бȯльшей степени удовлетворяющим условиям работы в системах обратной связи при управлении механизмами. В этом случае используются программные средства, обладающие при составлении решении уравнений, большей наглядностью, чем по методам [49–51]. А это важно для эффективного обучения персонала из разных групп подготовки, Заметим, что в Adams получить динамические характеристики не сложно, но проверка точности позиционирования положений [52–54] требует профессионального программирования, поэтому часть исследований проще произвести другими средствами, например в табличных процессорах. Имеем неизвестные реакции в узлах В и А Ry, Rx, Fy, Fx, Ру – является вычисляемой предельной нагрузкой, Рх – силой для имитации сопротивления перемещению груза, резания пород, и т. п. Ими можно моделировать любой вид нагрузки на манипуляторе, в том числе и динамический. В данном случае гидроцилиндры работают за счет движения штока, а также сдерживанием давления в момент, когда один из силовых гидроцилиндров с усилием F1 (СГ1) перемещает ведущее звено, а другой с усилием F2 (СГ2) удерживает связанные рычаги в заданном положении за счёт гидравлического замка, закрывающего полости и открывающего их при достижении предельного давления. Вычисления можно производить для случаев: поворота в точке В, когда второй гидроцилиндр установлен на замок и шарнир А не работает и для положения, когда заперт первый. Из схемы следуют соотношения:
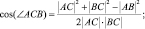 (2.1)
(2.1)
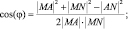 (2.2)
(2.2)
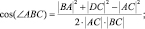 (2.3)
(2.3)
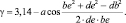 (2.4)
(2.4)
Для «запертого» СГ2:
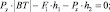 (2.5)
(2.5)
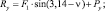 (2.6)
(2.6)
для «запертого» СГ1:
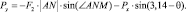 (2.7)
(2.7)
При динамическом характере движения следует добавить 5 инерциальных факторов от цилиндров и рычагов и груза, который несет манипулятор. Комплекс выражений, определяющих изменяемые значения в зависимости от положения механизма вводится в ячейки одной строки таблицы, а постоянные – в отдельный блок. Расчетные параметры в одной строке соответствуют одному положению механизма т. е. имеют однозначное соответствие. Задав, например, шаг изменения угла наклона ведущего звена (α) можно легко получить все вычисляемые параметры (их 24) для множества положений механизма практически с любой требуемой точностью при заданных выдвижениях штоков. Изменяя ход штока получим новые множества параметров. При этом автоматически выполняется построение графических зависимостей (рис. 2.7, а). Контроль решения легко производить и в Adams, (рис. 2.7, б), где можно получить и нагрузки и траектории, при бȯльших затратах времени. Таким образом, имея модели движения, получим характеристики нагрузок, действующие на гидроцилиндры по всей траектории переноса груза, а исходя из данных о мгновенных значениях координат, имеем величины хода штоков, а значит и характеристики расхода рабочей жидкости, направляемой в гидроприемники, что с учетом возможности рассчитать их по показаниям датчиков положения повышает надежность управления манипулятором. Так, для удержания детали LC в вертикальном положении, следует иметь зависимости углов от геометрических размеров деталей, составляющих удерживающую систему, которые в свою очередь определяются углами установки ξ и размерами рычагов:
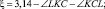 (2.8)
(2.8)
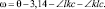 (2.9)
(2.9)
а
б
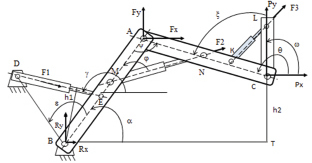
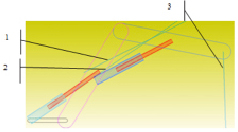
Рис. 2.7. Схема горного манипулятора несущего конструкцию LC: F1, F2, F3 – усилия гидроцилиндра для управления звеньями АВ, АС и конструкцией LC (а); BT, h1, h2 плечи сил; фото с экрана: имитация движения манипулятора в Adams: 1–3 – направления сил от гидроцилиндров и вертикальной нагрузки (б)
Если поставить требование на значение угла равное 90 градусов, (конструкция должна сохранять вертикальное положение) можно построить серию мгновенных положений механизма для получения расходных характеристик. Величина выдвижения будет зависеть и от силы сопротивления выдвижению, то есть от коэффициентов трения штоков и поршней и в шарнирах сочленения рычагов, что может привести к колебаниям и неточности установки, поэтому подачу жидкости следует осуществлять в полости индивидуально. Для сложной многозвенной геометрии манипулятора, например, с четырехзвенником Чебышева установить аналитические зависимости между параметрами сложно и не во всех случаях углы поворота звеньев сводятся к аналитическим выражениям. Поэтому они задаются от некоторого начального значения с заданным шагом, а затем для установки соответствия между параметрами для множества полученных данных выполняется фильтрация и сепарация из условия обеспечения целостности движения механизма и размещение сепарированных данных в единых строках таблицы [48]. В табличных процессорах используя VBA это легко выполнить с двойной точностью, чем обеспечивается и имитация точности обработки соприкасающихся поверхностей.
Выполним анализ НДС, цилиндра 1, штока с поршнем 2, 3 грунд-буксы 3, (рис. 2.8). На шток действуют следующие нагрузки: сила F, направленная по оси штока, в худшем случае она действует с некоторым смещением от оси (вследствие износа проушин или других причин); по поверхности поршня действует рабочее давление Qп, или давление срабатывания клапана гидрозамка. Со стороны штоковой полости Qs распределенно по кольцу. По поверхностям скольжения поршня и грунд-буксы действуют опорные реакции, направленные нормально к их поверхностям, (показаны силы трения Ftgb и Ftp от их действия, сила инерции Fi, равная произведению массы штока ms, поршня mp и жидкости mg на ускорение). Уравнение движения для СГ без учета момента в системе:
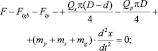 (2.10)
(2.10)
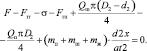 (2.11)
(2.11)
Задача существенно усложниться при введении давления в полостях как переменной величины в виде функции, зависящей от сечения сливного отверстия, скорости изменения движения, что в свою очередь зависит от характера изменения силы F, которая, в случае если производиться перемещение крепи в шахтном забое может быть существенно неравномерной. Наиболее опасный режим нагружения возникнет при выдвинутом штоке и максимальном эксцентрисистете. Тогда в системе возникает пара сил, вызывающая изгибные нагрузки на шток и поршень и повышение сил методики расчета на изгиб, распознавания и выявления характерных зон, для установки датчиков фиксирующих аномальное нагружение. Задача о расчёте НДС гидроцилиндра с МКЭ распадается на две: для штока и цилиндра, при переменном расстоянии между поршнем и началом координат. По периметрам грунд-буксы и поршня который скользит по поверхности цилиндра с коэффициентом трения 0,2, запрещены перемещения по осям Х и Y, а по площади дна поршня – перемещения по оси Z. Для цилиндра расчёт производиться при действии перед и за поршнем гидростатического давления Qs и Qp. Опыт эксплуатации показывает, что реальная нагрузка действует с эксцентриситетом, за счет абразивного износа шарнирных соединений. Имеется и специальная группа гидроцилиндров, в которых такой режим с эксцентриситетом считается нормальным (корректирующие гидроцилиндры проходческих полков, создающих усилия отклонения полка от стенки ствола), но методикой расчета это не учитывается. Это же можно отнести и к группе оборудования для вспомогательных монтажно-демонтажных работ, а также устройств, для разрушения материалов ударными нагрузками, когда рабочий инструмент имеет непосредственную связь с выдвижным элементом гидроцилиндра. Можно прогнозировать, что кроме изгибных нагрузок на штоки и цилиндры возникают и неравномерные контактные нагрузки по трущимся поверхностям в районе поршня и грунд-буксы. Особенно подвержены этим деформациям устройства, где отношение D/d максимально (табл. 4), где D – диаметр цилиндра, d – диаметр штока. Гидроцилиндры имеют срок службы до десятков лет, поэтому факторы неравномерного распределения нагрузок оказываются долго действующими. В этом случае актуален и вопрос области сосредоточения контактных нагрузок, поскольку на износ поверхности будут влиять как величина контактной нагрузки, так и время её действия. Поэтому необходим анализ особенностей взаимодействия контактирующих поверхностей. Например, для конструктивного выполнения с непосредственным контактом штока корректировочного домкрата с поверхностью ствола распределение множества индивидуальных контактов можно считать равновероятным по линии оконтуривающей диаметр штока и поршня. То есть износ всей трущейся поверхности равномерен, а вот для гидроцилиндров, работающих в фиксированном положении, когда исключены повороты штока относительно цилиндра, при закреплении этих элементов проушинами, велика вероятность того, что контакты и максимальное истирание будет происходить по определенным поверхностям в зависимости от зоны расположения деформации проушины. Расчет контактных моделей производим по методике [35, 37] созданием нескольких участков цилиндра в зонах расположения поршня и грунд-буксы, рабочей жидкости, вытесняемой из штоковой полости, и за поршнем с программным учетом движения отдельных элементов [51–57].
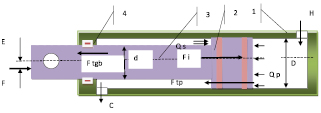
Рис. 2.8. Схема силового гидроцилиндра
Величина эксцентриситета принята исходя из деформаций проушин шахтных гидроцилиндров и достигает 0,04 м. Задача решается с учетом пластического деформирования в зоне контакта. Изгиб штока приводит к опорным реакциям в зоне контакта, как в балке на двух опорах. Получив контактные давления можно установить возможности износа поверхностей штока, гидроцилиндра и грунд-буксы. Напряжения на изгиб и контактные напряжения могут дать различныепо силе воздействия на конструкцию эффекты. Так по данным на рис. 4 контактные напряжения, достигающие трети от предела прочности, при полной безопасности штока от изгиба могут дать существенные ускорения износа трущихся поверхностей. Это позволяет уточнить причины выявленных в [58, 59] картин износа и особенности их идентификации. Программно-управляемые манипуляторы, выполненные в виде шарнирных рычагов, будут применяться при возведении анкерной крепи камер, зачистке кровли и почвы у сопряжений при подземной добычи. Разработаны и уточнены элементы моделирующего и тестирующего ПО для прогнозирования и управления их работой в режиме обратной связи. Уточнены методические элементы, картины нагружения в узлах и НДС, необходимые для распознавания аварийных ситуаций режимов работы гидроцилиндров, табл. 4.
а
б
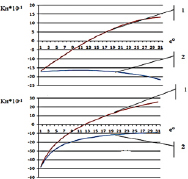
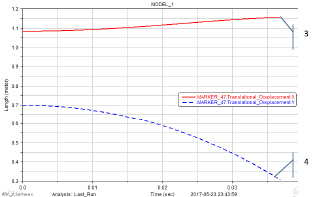
Рис. 2.9. Нагрузки, реакции и положение точки С (фото с экрана): 1 – реакция в шарнире В–Ry; 2 – Py нагрузка на манипулятор в зависимости от угла поворота рычага АВ при выдвижении штока гидроцилиндра MN, равном 0 м – а и 0,5 м – б, угол наклона рычага α = 81°–е°; перемещение точки (фото с экрана пакета Adams) С: 3 – по оси x; 4 – по оси y – с
Таблица 4
Отношение D/d в силовых гидроцилиндрах
|
Наименование |
D |
D первой ступени |
D второй ступени |
D/d |
|
Гидростойка крепи типа Глиник и др. |
1900 |
1600 |
1200 |
1,18/1,58 |
|
Домкраты корректировки |
1000 |
800 |
1,25 |
|
|
Домкраты передвижки |
1600 |
800 |
2 |
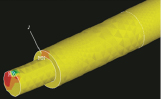
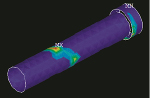
а б
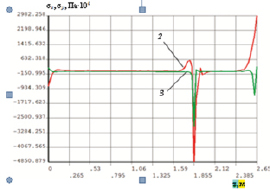
в
Рис. 2.10. НДС цилиндра и штока: а – ассиметрично нагруженная зона грунд-буксы1; б – зоны контактных давлений на штоке; в – распределение напряжений вдоль стенки цилиндра; 2 – σx; 3 – σу