Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Краткий конспект лекций по начертательной геометрии

Пиралова О. Ф., Ведякин Ф. Ф.,

1.3. Способы проецирования

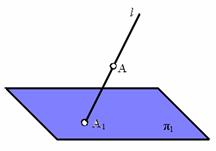
Проекцией точки А на плоскость проекций π₁ называется точка А₁ пересечения проецирующей прямой с плоскостью проекций π₁, проходящей через точку А, (рис. 1.1):

Проекция любой геометрической фигуры есть множество проекций всех ее точек. Направление проецирующих прямых и положение плоскостей π₁ определяют аппарат проецирования.

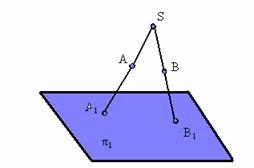
Центральным проецированием называется такое проецирование, при котором все проецирующие лучи исходят из одной точки S – центра проецирования (рис. 1.2).

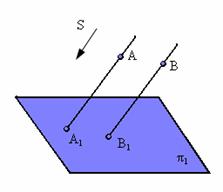
Параллельным проецированием называют такое проецирование, при котором все проецирующие прямые параллельны заданному направлению S (рис. 1.3).

.

Рис. 1.1. Проекция точки А на плоскость проекций π₁

.

Рис. 1.2. Пример центрального проецирования

.

Рис. 1.3. Пример параллельного проецирования

Параллельное проецирование представляет собой частный случай центрального проецирования, когда точка S находится на бесконечно большом расстоянии от плоскости проекций π₁.

При заданном аппарате проецирования каждой точке пространства соответствует одна и только одна точка на плоскости проекций.

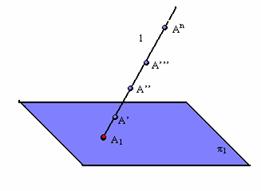
Одна проекция точки не определяет положения этой точки в пространстве. Действительно, проекции А₁ может соответствовать бесчисленное множество точек А^’, А^’’, …, расположенных на проецирующей прямой (рис. 1.4).

Для определения положения точки в пространстве при любом аппарате проецирования необходимо иметь две ее проекции, полученных при двух различных направлениях проецирования (или при двух различных центрах проецирования).

.

Рис. 1.4. Пример расположения множества точек на проецирующей прямой

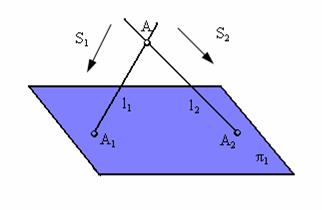
Так, из рис. 1.5 видно, что две проекции точки А (А₁ и А₂), полученные при двух направлениях проецирования S₁ и S₂ , определяют единственным образом положение самой точки А в пространстве – как пересечение проецирующих прямых ₁ и ₂, проведенных из проекций А₁ и А₂ параллельно направлениям проецирования S₁ и S₂.

.

Рис. 1.5. Определение положения точки А в пространстве