Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Краткий конспект лекций по начертательной геометрии

Пиралова О. Ф., Ведякин Ф. Ф.,

2.4. Следы прямой линии

.

а

.

б

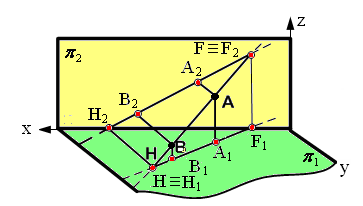
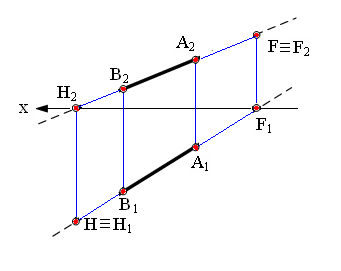
Рис. 2.11. Изображение следов прямой линии: а – в пространстве; б – на эпюре

Следом прямой линии называется точка пересечения прямой с плоскостью проекций.

В системе двух плоскостей проекций π₁ и π₂ прямая в общем случае имеет два следа:

1. Горизонтальный Н (Н₁, Н₂);
2. Фронтальный F (F₁, F₂)

Это точки пересечения прямой соответственно с горизонтальной и фронтальной плоскостями проекций.

Установим правило нахождения следов прямой.

Для нахождения горизонтального следа прямой необходимо:

1) продолжить фронтальную проекцию прямой а до пересечения с осью Х (получим точку Н_Х ≡ Н₂)

2) восстановить перпендикуляр в точке Н_Х к оси Х (провести линию связи перпендикулярную к оси Х);

3) продолжить горизонтальную проекцию прямой а до пересечения с перпендикуляром;

4) полученная точка пересечения и будет являться горизонтальным следом прямой а Н ≡ Н₁

Для нахождения фронтального следа прямой необходимо:

1) продолжить горизонтальную проекцию прямой а до пересечения с осью Х (точка F_X ≡ F₁);

2) восстановить перпендикуляр в точке F_X к оси Х;

3) продолжить фронтальную проекцию прямой до пересечения с перпендикуляром;

4) полученная точка пересечения F ≡ F₂ является фронтальным следом прямой а

В начертательной геометрии считается, что наблюдатель расположен в первом пространственном углу на бесконечном расстоянии от плоскостей проекций, поэтому видимыми геометрическими фигурами будут только те, которые расположены в первом октанте.

Проекции этих фигур в ортогональных и аксонометрических проекциях показываются сплошными линиями. Фигуры, расположенные в других пространственных углах, не видны наблюдателю, и их проекции показываются штриховыми линиями.