Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
7.3. Неразвертывающиеся (косые) линейчатые поверхности
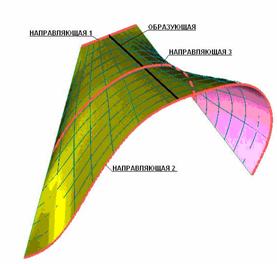
Неразвертывающиеся линейчатые поверхности в общем случае образуются движением прямолинейной образующей по трем направляющим линиям, которые однозначно задают закон ее перемещения (рис. 7.12).
Направляющие линии могут быть кривыми и прямыми. Общий случай линейчатой поверхности, как множества образующих прямых, пересекающих три заданные пространственные кривые показан на рис. 7.13.
.
.
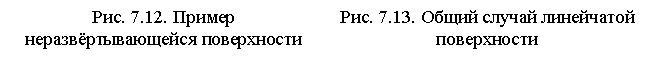Разновидностями косых поверхностей являются линейчатые поверхности с направляющей плоскостью и частные их виды − линейчатые поверхности с плоскостью параллелизма (поверхности Каталана).
В первом случае поверхность однозначно задается двумя направляющими линиями и направляющей плоскостью, которая заменяет третью направляющую линию. Образующая прямая скользит по двум направляющим и сохраняет постоянный угол α с некоторой плоскостью 
, которая называется направляющей. В частном случае, если угол равен нулю, образующая прямая будет параллельна направляющей плоскости, которая в этом случае называется плоскостью параллелизма.
Поверхности с направляющей плоскостью (α 
0) называются косыми цилиндроидами, если обе направляющие являются кривыми линиями; косыми коноидами - если одна из направляющих − прямая линия; дважды косой плоскостью, если направляющие − скрещивающиеся прямые.
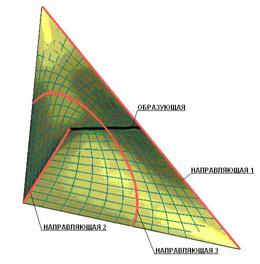
Дважды косой цилиндроид, как линейчатая поверхность с тремя направляющими, из которых две пространственные кривые и одна прямая показан на рис. 7.14.
На рис. 7.15. показан дважды косой коноид, образованный перемещением образующей прямой (красная) по трем направляющим, из которых две прямые. Показано построение одной образующей, как результата пересечения вспомогательной плоскости, проходящей через одну из прямолинейных направляющих, с двумя другими направляющими.
.
Рис. 7.14. Дважды косой цилиндроид
.
Рис. 7.15. Дважды косой коноид
Вопросы для самоконтроля
1. Как рассматриваются поверхности в начертательной геометрии?
2. Приведите краткую классификацию поверхностей, приняв за критерии классификации: а) вид образующей; б) характер перемещения образующей.
3. Что такое определитель поверхности? Что такое очерк поверхности?
4. Что значит «задать поверхность на чертеже»?
5. Сформулировать признак принадлежности точки поверхности.
6. Приведите примеры использования различных поверхностей в технике, науке, искусстве и других видах деятельности человека.