Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Краткий конспект лекций по начертательной геометрии

Пиралова О. Ф., Ведякин Ф. Ф.,

8.1. Пересечение поверхности плоскостью

Определение взаимного положения плоскости и поверхности – позиционная задача, для решения которой применяется метод вспомогательных секущих плоскостей. В качестве вспомогательных секущих плоскостей используются проецирующиеся плоскости – плоскости перпендикулярные плоскостям проекций, поэтому основу метода вспомогательных секущих плоскостей составляет алгоритм решения задачи по нахождению линии пересечения поверхности проецирующей плоскостью.

Особое место занимают задачи по нахождению линии пересечения плоскости с конической поверхностью. В зависимости от положения секущей плоскости линией пересечения может быть окружность, эллипс, парабола, гипербола.

Для определения проекции линии сечения следует найти проекции точек, принадлежащих этой линии в следующем порядке:

1) проекции опорных точек – точек расположенных на очерковых образующих поверхности (эти точки определяют границы видимости проекции кривой);

2) проекции экстремальных точек, удаленных на минимальные и максимальные расстояния от плоскостей проекций;

3) проекции произвольных (промежуточные) точек линии сечения.

В зависимости от положения плоскости по отношению к плоскостям проекций, сложность решения позиционной задачи, по определению линии пересечения ее с поверхностью существенно меняется. Наиболее простым представляется случай, когда плоскость проецирующая, поэтому к рассмотрению предлагается пример пересечения поверхности проецирующей плоскостью

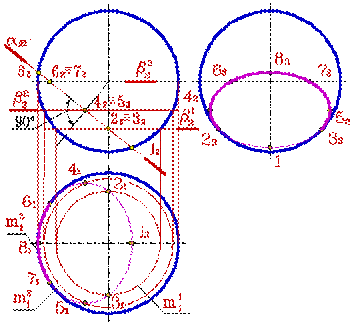
Окружность, по которой плоскость α пересекает сферу, проецируется на плоскости П₁ и П₃ в виде эллипса, а на плоскость П₂ в прямую линию ограниченную очерком сферы.

Охарактеризуем выбранные для построения точки:

1, 8 – две вершины эллипса, определяющие положение малой оси на горизонтальной и профильной проекциях, их фронтальные проекции определяют пересечение следа плоскости α с очерком сферы. Эти точки являются соответственно высшей и низшей точками сечения.

2, 3 – фронтальные проекции этих точек лежит на вертикальной оси сферы, а профильные проекции будут лежать на очерке сферы и определять зону видимости при построении эллипса на П₃.

4, 5 – две вершины эллипса, определяющие положение большой оси эллипса на горизонтальной и профильной проекциях, положение их фронтальной проекции определяет перпендикуляр, опущенный из центра сферы к следу плоскости α.

.

а

.

б

Рис. 8.1. Изображение пересечения поверхности сферы проецирующей плоскостью: а − изображение в пространстве; б − изображение на комплексном чертеже

6, 7 – фронтальные проекции этих точек лежат на горизонтальной оси сферы, т.е. принадлежат экватору сферы, их горизонтальная проекция лежит на очерке сферы и определяет зону видимости при построении эллипса на П₁.

Линия пересечения плоскости α и сферы на фронтальной плоскости проекций совпадает со следом плоскости α, на ней отмечаем точки 1₂…8₂. Для нахождения горизонтальных проекций этих точек в общем случае используется метод вспомогательных секущих плоскостей (β- горизонтальные плоскости уровня). Например, через точки 2₂, 3₂ проведем след плоскости β¹₂, на горизонтальной плоскости проекций линией пересечения плоскости β₁ и сферы будет окружность m₁¹, а точки 2₁ и 3₁ лежат на этой окружности по линии связи (в данном случае осевой линии). Таким образом находятся все точки, кроме 1₁ и 8₁ , которые ввиду своего положения на очерке фронтальной проекции сферы будут принадлежать горизонтальной осевой линии на плоскости П₁. Построенные точки 1₁…8₁ соединим плавной кривой линией с.

Особое место занимают задачи по нахождению линии пересечения плоскости с конической поверхностью. В зависимости от положения секущей плоскости линией пересечения может быть окружность, эллипс, парабола.