
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
8.2. Конические сечения
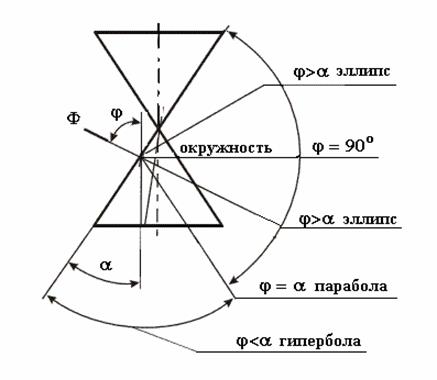
В зависимости от положения секущей плоскости линиями сечения конической поверхности могут быть: эллипс, парабола, гипербола и окружность а в частных случаях: прямая, две пересекающиеся прямые и точка (рис. 8.3).
 .
.
 .
.
Рассмотрим некоторые примеры пересечения конуса плоскостью.
Если плоскость Ф пересекает все образующие поверхности конуса вращения, т.е. если φ>α, то линией сечения является эллипс (рис. 8.3 а). В этом случае секущая плоскость не параллельна ни одной из образующих поверхности конуса.
Если плоскость Ф параллельна основанию поверхности конуса, то линией пересечения является окружность (рис. 8.3.б).
 .
.
a
 .
.
б
 .
.
в
 .
.
г
Рис. 8.3. Изображение линии сечения поверхности конуса плоскостью: а – эллипса; б – окружности; в – параболы; г – гиперболы
Если плоскость Ф параллельна одной образующей поверхности конуса, т.е. φ=α, то линией пересечения является парабола (рис.8.3.в). В частном случае (плоскость является касательной к поверхности конуса) сечение вырождается в прямую.
Если плоскость Ф параллельна двум образующим поверхности конуса (в частном случае параллельна оси конуса), т.е. φ<α, то линией сечения является гипербола (рис. 8.3. г). В случае прохождения плоскости через вершину конической поверхности фигурой сечения могут быть сами образующие, т.е. гипербола вырождается в две пересекающие прямые.
