Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Краткий конспект лекций по начертательной геометрии

Пиралова О. Ф., Ведякин Ф. Ф.,

9.2. Построение разверток многогранников

Развертка многогранника представляет собой плоскую фигуру, полученную при совмещении всех его граней с плоскостью. Следовательно, построение развертки многогранника сводится к построению истинных величин его граней. Выполнение этой операции связано с определением натуральных величин его ребер, которые являются сторонами многоугольников – граней, а иногда и некоторых других элементов. Ребра многогранника условно разделяются на боковые и стороны основания. Существуют три способа построения разверток многогранных поверхностей:

1) способ треугольников (триангуляции);

2) способ нормального сечения;

3) способ раскатки.

Построение развертки пирамиды способом триангуляции

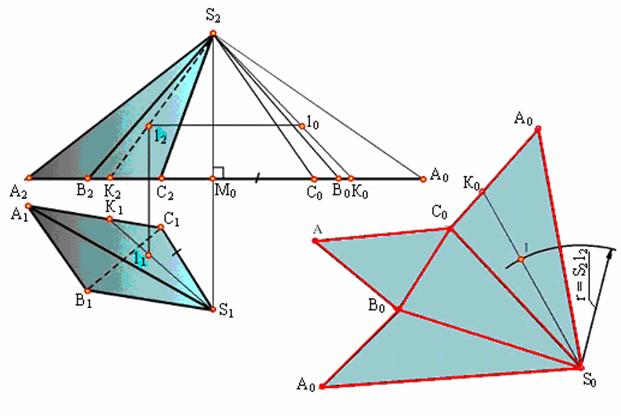
Боковые грани любой пирамиды являются треугольниками. Для построения развертки пирамиды (рис. 9.2) необходимо предварительно определить натуральные величины боковых ребер и сторон основания.

.

Рис. 9.2. Построение развертки пирамиды

У изображенной на рисунке пирамиды стороны основания являются горизонталями и проецируются на плоскость П₁ в истинную величину. Истинные величины боковых ребер определены способом прямоугольных треугольников. S₂M₀C₀, S₂M₀B₀ и S₂M₀А₀, у которых одним катетом является высота пирамиды (S₂М₀ - разность высот точки S и точек А, В, С), а другим - горизонтальная проекция соответствующего ребра.

(/M₀C₀/ = /S₁C₁/; /M₀B₀/ = /S₁B₁/; /M₀A₀/ = /S₁A₁/; /M₀K₀/ = /S₁K₁/).

Натуральные величины ребер пирамиды могут быть определены способом вращения вокруг оси, проходящей через вершину S и перпендикулярной плоскости П₁.

Следующая операция состоит в построении каждой боковой грани как треугольника по трем сторонам. В результате получается развертка боковой поверхности пирамиды в виде ряда примыкающих друг к другу треугольников с общей вершиной S. Присоединив к полученной фигуре основание (АВС), получим полную развертку пирамиды. Построение на развертке точки 1, принадлежащей поверхности пирамиды, понятно из чертежа. Такой способ построения развертки поверхности называется способом триангуляций.

Построение развертки призмы способом нормального сечения

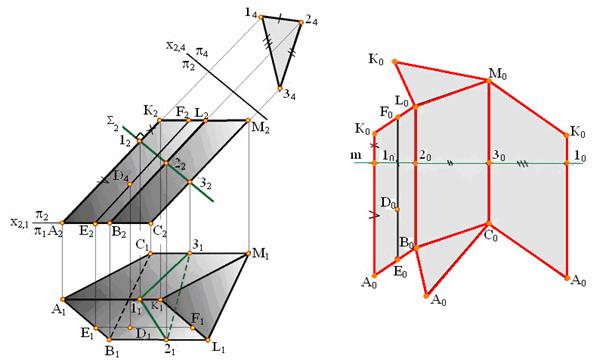
Для построения развертки наклонной призмы, изображенной на рис. 9.3 необходимо найти истинные величины боковых ребер и сторон основания призмы. Призма расположена так, что ее боковые ребра параллельны плоскости П₂ и проецируются на нее в натуральную величину. Стороны оснований являются горизонталями и проецируются на плоскость П₁ без искажения. Таким образом, длины сторон каждой грани известны, однако этого еще недостаточно для построения истинной формы боковых граней.

.

Рис. 9.3. Построение развертки призмы

Боковые грани наклонной призмы являются параллелограммами, которые не могут быть построены по четырем сторонам. Для построения параллелограмма необходимо помимо длины сторон знать еще его высоту. Для определения высот граней пересечем призму плоскостью (₂), перпендикулярной к ребрам (способ нормального сечения), и определим истинную величину сечения путем замены плоскостей проекций. Стороны этого нормального сечения и будут высотами соответствующих граней. Теперь приступаем к построению развертки. На свободном месте чертежа проводим горизонтальную прямую m и откладываем на ней отрезки /1 - 2/ = /1₄ - 2₄/, /2 - З/ = /2₄ - 3₄/ и /3 - 1/ = /3₄ - 1₄/.

Через точки 1, 2, 3, 1 проводим перпендикуляры к прямой m и откладываем на них величины боковых ребер так, чтобы /А1/ = /А₂1₂/ и /1К/ = /1₂К₂/, /В2/ = /В₂2₂/ и /2L/ = /2₂L₂/ и т. п.

Соединив концы построенных отрезков, получим развертку боковой поверхности призмы. Присоединив к ней оба основания, получим полную развертку призмы. Построение на развертке точки 4, принадлежащей поверхности призмы, понятно из чертежа.