
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
10.2. Пример построения касательной к поверхности
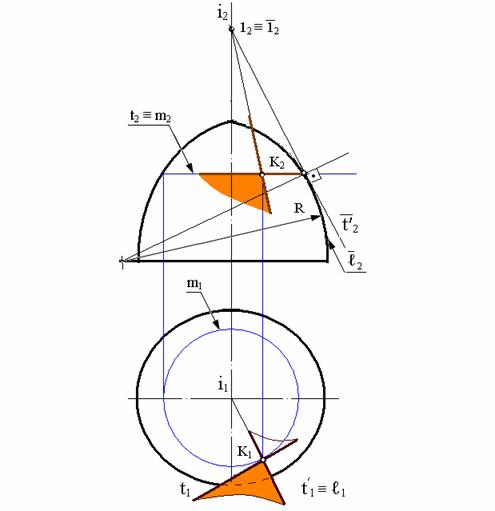
Рассмотрим на рис. 10.3 пример построения касательной плоскости к поверхности тора α в точке К.
Через точку К проведем две прямые t и t′. Прямая t1 касательная к параллели тора m, которая является окружностью, проходящей через точку К. Прямая t′ касательна к меридиану ![]() , проходящему через эту точку. Для проведения касательной t′ к меридиану
, проходящему через эту точку. Для проведения касательной t′ к меридиану ![]() совмещаем его с главным меридианом
совмещаем его с главным меридианом ![]() вращением вокруг оси тора. В этом положении к нему через точку
вращением вокруг оси тора. В этом положении к нему через точку ![]() проводим касательную t′ . Поворот ее в обратном направлении дает искомую линию t′ .На рисунке она определена неподвижной точкой, в которой касательная t′ пересекает ось тора (1≡1), и заданной точкой К.
проводим касательную t′ . Поворот ее в обратном направлении дает искомую линию t′ .На рисунке она определена неподвижной точкой, в которой касательная t′ пересекает ось тора (1≡1), и заданной точкой К.
Прямые t и t′ определяют искомую плоскость τ.
 .
.
Рис. 10.3. Пример построения касательной плоскости к поверхности тора
Вопросы для самопроверки
1. Что называется касательной плоскостью к поверхности?
2. Что называется нормалью?
3. В чём сущность использования касательных?
