Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
Измерение загрязнённости речной воды (на примере малой ре-ки Малая Кокшага)
Сибагатуллина А. М., Мазуркин П. М.,
2.6. Обработка результатов измерений
Обработка прямых измерений. Для характеристики большинства приборов часто используют понятие приведенной погрешности, равной абсолютной погрешности в процентах диапазона шкалы измерений. По приведенной погрешности приборы разделяются на классы точности. Класс точности указан на панели прибора.
Наибольшая инструментальная погрешность измеряется по формуле:
, (2.1)
где К – класс точности, А – наибольшее значение шкалы прибора.
Инструментальную погрешность невозможно уменьшить статистической обработкой отсчетов.
При наличии случайных погрешностей наблюдаемые значения измеряемой величины при многократных измерениях случайным образом рассеяны относительно ее истинного значения. В этом случае действительное значение находят как наиболее вероятное из серии отсчетов, а погрешность характеризуют шириной интервала, который с заданной вероятностью показывает истинное значение [44].
Наилучшей оценкой истинного значения величины Х является выборочное среднее значение
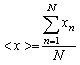, (2.2)
где 
– отсчет величины Х, – число отсчетов.
Для оценки разброса отсчетов при измерении используется выборочное среднее квадратическое отклонение отсчетов
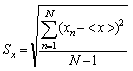. (2.3)
Выборочное среднее является случайной величиной и его разброс относительно истинного значения измеряемой величины оценивается выборочным средним квадратическим отклонением среднего значения
. (2.4)
Доверительным интервалом называется интервал 
, который с заданной степенью достоверности включает в себя истинное значение измеряемой величины.
Доверительной вероятностью (надежностью) результата серии наблюдений называется вероятность 
, с которой доверительный интервал включает истинное значение измеряемой величины.
Случайную составляющую погрешности принято выражать как полуширину доверительного интервала. Случайная составляющая погрешности многократных измерений
, (2.5)
где 
– безразмерный коэффициент доверия (коэффициент Стьюдента).
Чем больше доверительная вероятность, тем надежнее оценка интервала и, вместе с тем, шире его границы.
Полная абсолютная погрешность 
прямых измерений равна квадратической сумме ее составляющих: инструментальной – 
и случайной – 
. (2.6)
Полная относительная погрешность 
прямых измерений равна отношению полной абсолютной погрешности к выборочному среднему значению
. (2.7)
Обработка косвенных измерений [44]. Расчет погрешностей косвенных измерений осуществляется по алгоритму, использующему сложение абсолютных величин погрешностей.
Пусть 
– функциональная зависимость между измеряемой величиной 
и величинами 
, значения которых найдены прямыми измерениями. Действительное значение 
определяется как:
. (2.8)
Вычисляем относительные погрешности аргументов. Затем определяем абсолютную и относительную погрешности функции
(2.9)
и по формулам:
- для относительной погрешности
; (2.10)
- для абсолютной погрешности
. (2.11)
Оценка токсического действия тестируемой пробы воды. Оценка токсического действия тестируемой пробы воды делается на основании достоверности различий между показателями прироста численности клеток водорослей в контроле и в опыте. При этом вычисляют [14]:
– средние арифметические величины прироста численности клеток – Xi и X (в контроле и опыте);
– среднее квадратичное отклонение по формуле 
(2.3);
– ошибку среднего арифметического (X):
– Td – критерий достоверности различий двух величин:
; (2.12)
, (2.13)
где xk и xо – сравниваемые средние величины (в контроле и опыте),
Sk2 и So2 – квадраты ошибок средних в контроле и опыте.
Td рассчитывают для каждой тестируемой пробы и сравнивают с табличной величиной Tst – стандартным значением критерия Стьюдента. В нашем случае для его определения принимаем уровень значимости р = 0,05 (95%) и степень свободы = (n1 + n2 – 2), т. е. (3 + 3 – 2) = 4. Tst при степени свободы 4 равно 2,78.
Если Td ≥ Tst, то различие между контролем и опытом достоверно – тестируемая вода загрязнена.
Если Td < Tst, то различие между контролем и опытом не достоверно – тестируемая вода не загрязнена.