Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Методы структурно-параметрического синтеза энергетически напряженных сложных функциональных блоков, систем на кристалле

Манжула В. Г.,

1.2 Анализ энергетических характеристик преобразовательного элемента

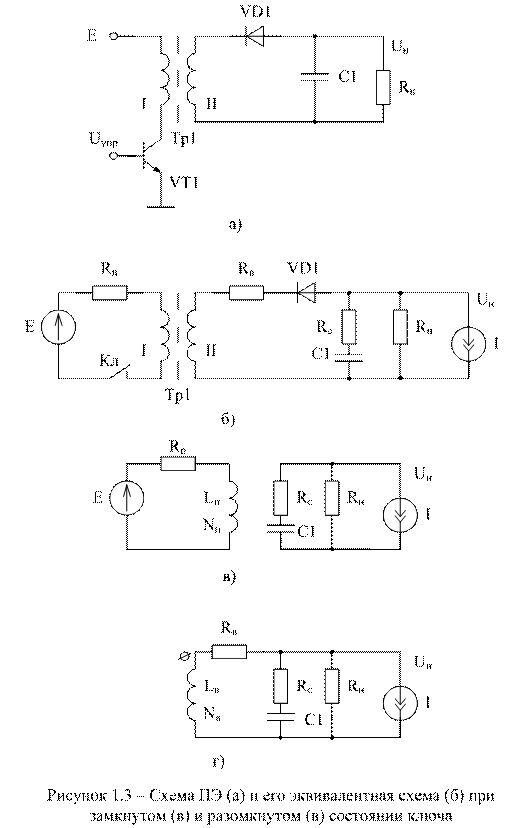
Рассмотрим однотактный преобразовательный элемент (ПЭ) с трансформаторной развязкой между входом и выходом (рис.1.3.а). Он состоит из ключа - транзистор VT1, выпрямителя - диод VD1, высокочастотного фильтра - конденсатор С1, накопительного трансформатора ТР1 с первичной обмоткой I и вторичной - II. Роль нагрузки выполняет резистор R . Ключ управляется напряжением U_упр при высоком потенциале ключ замкнут, при низком - разомкнут. Проведем анализ такой схемы с целью определения ее основных характеристик и параметров элементов в установившемся режиме. Для анализа воспользуемся методом усреднения пространства состояний,

дающим компромисс между точностью результатов и простотой математического аппарата [22,23].

Данную структуру (рис.1.3.а) можно представить в виде эквивалентной схемы, изображенной на рис.1.3.б. В ней резистор R_п учитывает активное сопротивление реального ключа Кл, обмотки I и источника питания Е; резистор R_в - активное сопротивление обмотки II и дифференциальное сопротивление диода VD1; резистор R_с - активное сопротивление конденсатора С1. Источник тока i_о- эквивалент изменения сопротивления нагрузки. Потери в сердечнике не учитываются.

При работе ПЭ имеет два устойчивых состояния: в первом ключ замкнут на время D₁ Т, и идет накопление энергии в обмотке I; во втором ключ разомкнут на время D₂ Т , и энергия от входного источника не потребляется (D₁, D₂ - относительные длительности замкнутого и разомкнутого состояния ключа; Т - период коммутации). Соответственно для каждого из состояний эквивалентная схема (рис.1.3.б) преобразуется к виду, представленному на рис.1.3-в,г.

.

В первом состоянии ПЭ описывается следующими выражениями:

, (1.5)

где 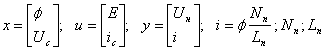- число витков и индуктивность первичной обмотки; Е, U_н - напряжение источника питания и нагрузки. Основными переменными являются магнитный поток в сердечнике трансформатора Ф и напряжение на конденсаторе U_с. Исключая переменную i, выражения (1.5) запишем в следующем виде:

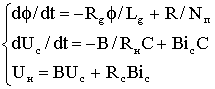(1.6)

где . Решая уравнение (1.6) получаем

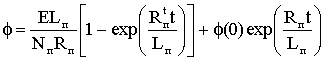(1.7)

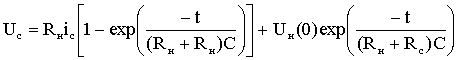, (1.8)

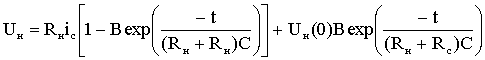. (1.9)

где Ф(0), U_с (0) - магнитный поток и напряжение на емкости в начальный момент времени. Для усреднения данных величин на интервале времени от 0 до D₁Т проинтегрируем выражения (1.7)-(1.9). Полагая, что

где и„_д - среднее значение напряжения U__ на интервале от О до D Т.

,

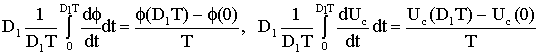получаем:

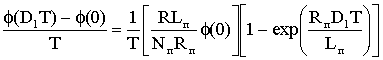, (1.10)

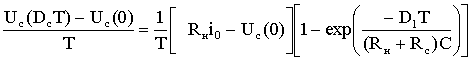,(1.11)

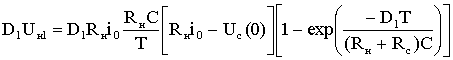(1.12)

где U_н1 – среднее значение напряжения U_н на интервале от 0 до D₁T.

Во втором состоянии ПЭ описывается следующими выражениями:

, (1.13)

исключая переменную i, аналогично первому состоянию, получаем:

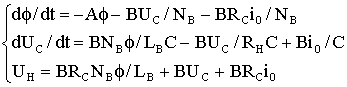, (1.14)

где А=(R_B+R_СB)/L_B; N_B, L_B - число витков и индуктивность вторичной обмотки. Решения этих уравнений можно записать в следующем виде:

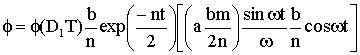(1.15)

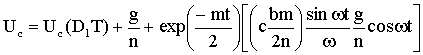(1.16)

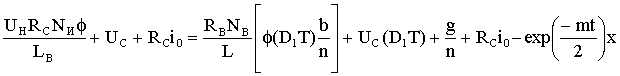
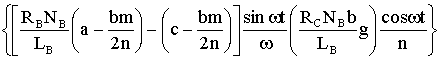, (1.17)

где , , ,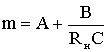

, .

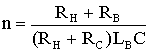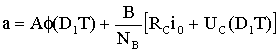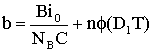После интегрирования выражений (1.15)-(1.17) и умножения на D₂ получаем усредненное изменение величин за второй интервал:

.

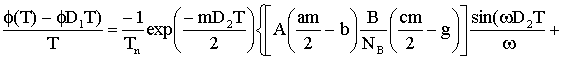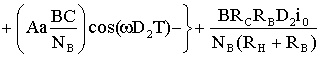, (1.18)

.

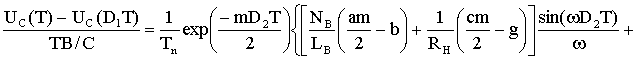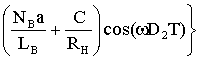, (1.19)

.

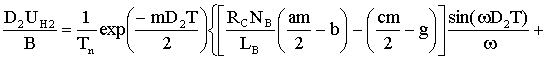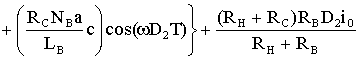, (1.20)

где U_н2 –среднее значение напряжения U_н на интервале от D₁Т до Т . Суммируя левые члены выражений (1.10) и (1.18), получаем выражение (1/Т)(ф(Т)-ф(0)). Аналогично получаем выражение для переменной Uс. Далее полагаем, что ф и U_с – это средние значения ф (кТ) и U_с(кТ). Для простоты будем использовать обозначение ф*=ф(кТ+D₁Т). Определяя значения величин в установившемся режиме (путем замены E→Е+е и т.д. с по следующей линеаризацией), получаем:

.

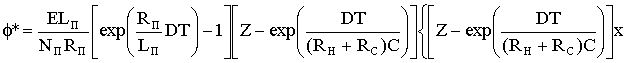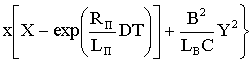(1.21)

.

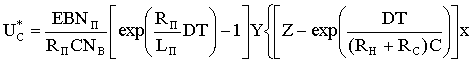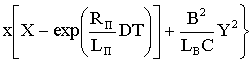(1.22)

.

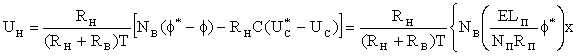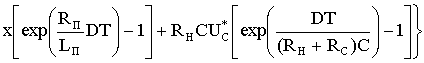(1.23)

где,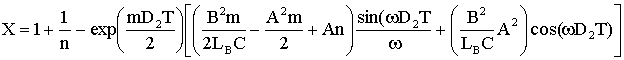

,

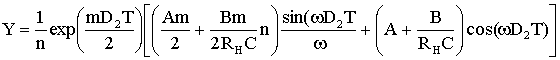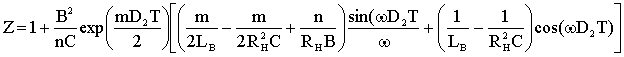
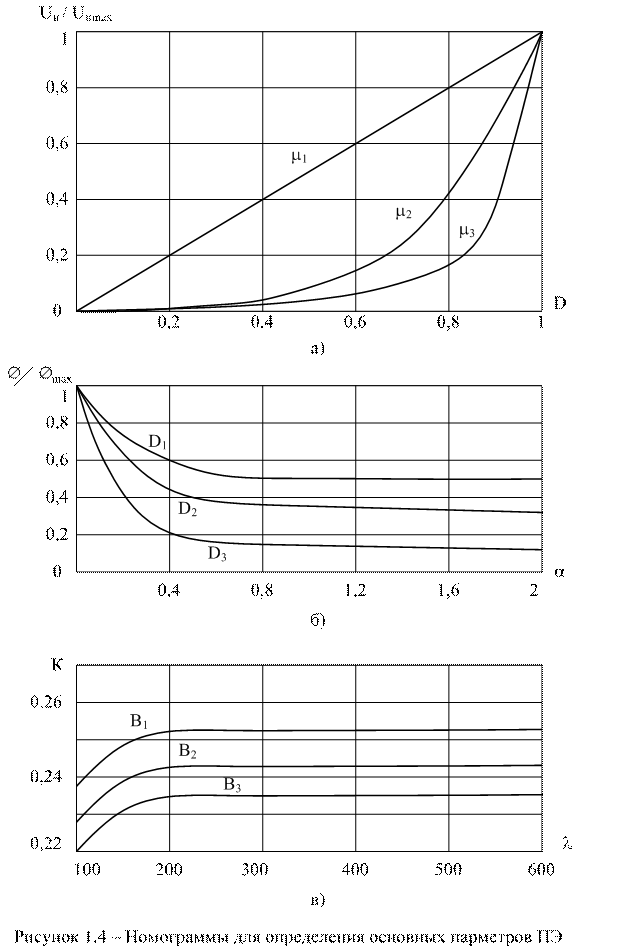
На основании выражений (1.21)-(1.23) при следующих параметрах элементов: Е= 20 В, L_П=5мГн, L_B= 0,1 мГн, N_П= 100, N_B= 45, R_C= 75 мОм построены номограммы (рис.1.4.а-в). Нормированная регулировочная характеристика (рис.1.4.а) отражает зависимость выходного напряжения от величины относительной длительности импульса D и относительной постоянной времени m цепи накопления энергии (m = t_нак/T=L_П/R_П, где t_нак - постоянная времени цепи накопления энергии). Из рассмотрения графика на рис. 1.4.а (m₁=6, m₂=0,6, m₃=0,33) очевидно, что для получения широкого диапазона регулирования ПЭ коэффициент m следует выбирать существенно большим 1, однако для получения более высокой крутизны преобразования, коэффициент m должен быть меньше 1, но при этом существенно снижается линейность регулировочной характеристики и диапазон регулирования ПЭ. Таким образом, если в начальных условиях задан параметр t_{нак ,} то частоту преобразования необходимо выбирать из условия получения требуемой зависимости регулировочной характеристики и наоборот.

.

Из рассмотрения зависимости (рис.1.4.б) величины магнитного потока от относительной постоянной времени цепи отдачи энергии из трансформатора a (a=T/t_отд, где t_отд=1/А – постоянна времени цепи отдачи энергии) и относительной длительности импульса (D₁=0,6 D₂=0,3, D₃=0,01) можно сделать следующие выводы. Вариация относительной постоянной времени a оказывает меньшее влияние на величину магнитного потока в сердечнике, в случае если ПЭ работает с повышенным значением параметра D. При этом достигается большая стабильность частоты преобразования. Но при фиксированной частоте преобразования повышается вероятность насыщения сердечника. Таким образом, при фиксированной частоте преобразования рекомендуется работать при пониженном значении параметра D, а в автоколебательном режиме - при повышенном значении D.

Зависимость (рис.1.4-в) коэффициента передачи К (K=U_н /E) ПЭ от величины относительной постоянной времени цепи отдачи энергии (l=/T=C(R_н+R_с)/T, где t_p - постоянная времени отдачи энергии из емкости) от параметра В (В₁ =0,997, В₂ =0,996, В₃ =0,995) показывает, что величина параметра В влияет на коэффициент К, а параметр l не оказывает воздействия на величину коэффициента К при условии l »Т. Таким образом, параметр l необходимо выбирать из условия: l >200 для исключения влияния величины сопротивления R_н на выходное напряжение ПЭ.