Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Моделирование конкуренции в условиях рынка

Степанов Л. В.,

3.3.2 Формализация ценовых и неценовых характеристик товара

Как отмечалось выше, каждый товар  t_k  может иметь свой набор характеристик {h_k^y} , что отражается наличием индекса k у элементов множества H. Кроме того:

где C - ценовые характеристики, а NC - неценовые характеристики товара.

К ценовым характеристикам C можно отнести: цена товара - это денежный эквивалент товара, который устанавливает продавец и платит покупатель за право владения товаром; затраты на установку товара; затраты на гарантию и обслуживание; затраты на обучение персонала; затраты на потребление электроэнергии; затраты по замене устаревшей на более современную модель; какие-либо скидки за приобретение именно этого товара и другие.

Важно отметить, что ценовые характеристики имеют числовое выражение                   (в большинстве случаев - «рублевое»). Для расчета этих показателей используют подходы маркетинга и, в частности, методики теории ценообразования.

К неценовым характеристикам NC можно отнести: выгоды торговой марки и дизайна; качество сопутствующего обслуживания; удобство доставки; имидж марки компании; эксплуатационные показатели; надежность; эстетика товара и другие.

В отличии от ценовых, неценовые характеристики не имеют числового выражения и представляют собой качественные описания.

Причем для каждого товара перечень всех характеристик определен и постоянен для любого рынка. Этот перечень устанавливается производителем, как совокупность некоторых сервисов, предоставляемых им потребителям на данном рынке.

Только в совокупности ценовые и неценовые характеристики дают полное описание всех свойств и особенностей товара. Использование одних в отрыве от других позволит получить неполную картину описания товара, что понизит осведомленность и может привести к недобросовестной конкуренции (определение 15).

Для перехода к единой системе оценок товара предлагается воспользоваться положениями теории принятия решений и нечетких множеств, сформулировав их применительно к задаче конкуренции.

Как отмечалось выше, вероятностный подход не может быть признан надежным и адекватным инструментом решения слабоструктурированных задач [57, 59], к которым принадлежит и рассматриваемая проблема. В принципе, любая попытка использования статистических методов для решения такого рода задач - есть искусственный переход к хорошо структурированным (хорошо формализованным) задачам, при этом такой переход существенно искажает исходную постановку задачи. Ограничения и недостатки применения «классических» формальных методов при решении слабоструктурированных задач являются следствием сформулированного основоположником теории нечетких множеств Л.А. Заде [133] «принципа несовместимости»: «...чем ближе мы подходим к решению проблем реального мира, тем очевиднее, что при увеличении сложности системы наша способность делать точные и уверенные заключения о ее поведении уменьшаются до определенного порога, за которым точность и уверенность становятся почти взаимоисключающими понятиями» [50 ,51].

Методы, базирующиеся на теории нечетких множеств и теории принятия решений, весьма эффективны в условиях неопределенности. Их использование предполагает формализацию исходных параметров и целевых показателей эффективности в виде вектора интервальных значений (нечеткого интервала), попадание в каждый интервал которого, характеризуется некоторой степенью неопределенности. На основе исходной информации, опыта, и интуиции эксперты часто могут достаточно уверенно количественно охарактеризовать границы (интервалы) возможных (допустимых) значений параметров и области их наиболее возможных (предпочтительных) значений.

С позиции теории принятия решений множество характеристик товара H можно определить, как вектор критериев. Тогда  - y-й критерий оценки качества товара.

Так как ценовые показатели привлекательности можно точно оценить численным значением пропорциональным показателю, то их будем считать количественными C. Неценовые характеристики нельзя точно связать с каким-либо числом. В этом случае их будет считать качественными критериями NC. Следовательно, проблемы выбора оптимальных характеристик товара представляет собой многокритериальную задачу, а основная сложность ее решения заключается в присутствии качественных критериев, которые представляют собой лингвистические конструкции, описывающие то или иное свойство товара.

Понятие нечеткого множества - это попытка математической формализации нечеткой информации для построения математических моделей [59, 51, 81]. В основе этого понятия лежит представление о том, что составляющие данное множество элементы, обладающие общим свойством, могут обладать этим свойством в различной степени и, следовательно, принадлежать к данному множеству с различной степенью.

Согласно [51]:

• 1. Лингвистической переменной называется переменная, значениями которой могут быть слова или словосочетания некоторого естественного или искусственного языка.
• 1. Терм-множеством называется множество всех возможных значений лингвистической переменной.
• 2. Термом называется любой элемент терм-множества. В теории нечетких множеств терм формализуется нечетким множеством с помощью функции принадлежности.

Рассмотрим переменную «скорость автомобиля», которая оценивается по шкале «низкая», «средняя», «высокая» и «очень высокая». В этом примере лингвистической переменной является «скорость автомобиля», термами - лингвистические оценки «низкая», «средняя», «высокая» и «очень высокая», которые и составляют терм-множество.

В соответствии с положениями данной задачи введем определение.

Определение 17. Качественным критерием назовем показа­тель привлекательности товара, выраженный одной или множеством лингвистических конструкций (слово или словосочетание) естественного или искусственного языка, принятого в той или иной предметной области.

Тогда для каждого  можно согласно определению 17, задать множество лингвистических конструкций L^y, максимально полно описывающее все значения, которые может принимать y-й критерий:

,                        (3.23)

где r - количество лингвистических конструкций y-го критерия товаров монополиста.

Важно отметить, что шкала и значения  L^y по каждому из качественных критериев h^y не меняются при их рассмотрении с позиции монополиста и потребителя (потребителей). Это подтверждается особенностями монопольной конкуренции, как «диктата» одного лица всему рынку. Потребители не могут непосредственно определять параметры производимого товара. Они могут лишь регулировать свою потребность в нем и выбирать наиболее желаемые характеристики из предложенных монополистом.

Для перехода к числовым характеристикам необходимо поставить в соответствие каждому l_b некоторую оценку, характеризующую ее вес по отношению к другим :                            

Тогда появляется возможность использовать эти оценки наравне или вместо лингвистических терминов  в расчетах, в сравнении и так далее.

Однако на практике не всегда можно точно и пропорционально оценить показатели привлекательности, особенно при их большом числе.

Предлагается сравнить попарно все имеющиеся и оценить, насколько одна  отличается другой.

Зададим независимую шкалу, характеризующую степень отличия и состоящую из пар «ОПИСАНИЕ: СТЕПЕНЬ ПРЕДПОЧТИТЕЛЬНОСТИ»:

                            (3.25)

где dl - количество степеней предпочтительности.

Каждый элемент  sh_u является целым числом, значение которого характеризует степень отличия op двух любых величин. В зависимости от требуемой точности эта шкала может быть любой длины dl, а ее элементы  sh_u  могут быть заданы с любым одинаковым шагом.

На основе метода аналитической иерархии [18, 46, 105, 71, 76], построим квадратную матрицу попарного сравнения SR лингвистических конструкций l_b:

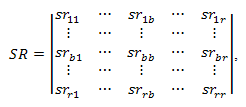,              (3.26)

где

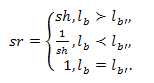                                         (3.27)

Примечание: Здесь символ означает предпочтительность, то есть одна лингвистическая конструкция лучше другой.

Используя матрицу попарного сравнения SR, можно определить значение веса каждой лингвистической конструкции  несколькими способами [91].

Способ 1:

• 1. Суммируем элементы строк матрицы попарного сравнения:

                  (3.28)

где b и b' - индексы строки и столбца соответственно.

• 2. Определяем сумму всех элементов матрицы сравнения SR:

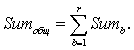              (3.29)

• 3. Нормализуем значения:

                        (3.30)

Способ 2:

• 1. Умножаем элементы строк матрицы SR и вычисляем r-й корень из произведения:

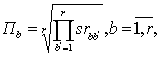                   (3.31)

где b и b' - индексы строки и столбца соответственно.

• 2. Определяем сумму:

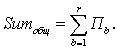                  (3.32)

• 3. Нормализуем значения:

                        (3.33)

Оба способа несложно реализовать даже при большой матрице SR. Однако, второй способ предпочтительнее, так как позволяет получить более точную оценку веса по шкале.

В результате можно получить числовой вектор характеристических значений для каждой лингвистической конструкции L^y.

Применение (3.23)-(3.33) позволяет найти весовые значения для каждого неценового критерия h^y, а далее и всех товаров множества T.

Для повышения наглядности эффективности предложенных методик рассмотрим пример формализации неценовых характеристик. Пусть производитель выпускает три товара (Товар₁, Товар₂, Товар₃) со следующими установленными характеристиками:

• 1. ценовые: цена; затраты на установку товара; затраты на гарантию; затраты на электроэнергию; затраты на обучение; затраты по замене.
• 2. неценовые: имидж марки компании; удобство доставки; качество обслуживания; надежность; эксплуатационные показатели; эстетика товара.

Будем считать, что у данных товаров других характеристик не существует, либо они не важны для потребителей этих товаров. Также будем полагать, что характеристики товаров различаются (табл. 3.1).

Таблица 3.1

Характеристики товаров монополиста

Ценовые характеристики
	Цена	Затраты на установку товара	Затраты на гарантию	Затраты на электроэнергию	Затраты на обучение	Затраты по замене
Товар1	200,00р.	65,00р.	48,00р.	0р.	0р.	0р.
Товар2	657,00р.	0р.	0р.	89,00р.	98,00р.	0р.
Товар3	489,00р.	36,00р.	0р.	0р.	0р.	14,00р.

Неценовые характеристики
	Имидж марки компании	Удобство доставки	Качество обслуживания	Надежность	Эксплуатационные показатели	Эстетика товара
Товар1	неизвестная	среднее	-	-	хорошие	-
Товар2	известная	высокое	высокое	низкая	-	-
Товар3	средне	-	среднее	-	отличные	привлекательный

Ценовые характеристики товаров (табл. 3.1) в формализации не нуждаются, так как изначально имеют числовое выражение.

Первым неценовым критерием  h¹ является имидж марки компании. Пусть согласно (3.23) его можно охарактеризовать множеством лингвистических конструкций:

L¹ = {Известная, Средне, Неизвестная}                      (3.34)

В соответствии с (3.25) можно задать шкалу важности:

Таблица 3.2

Шкала сравнения

Уровень op	Степень предпочтительности sh
Равная важность	1
Умеренное превосходство	3
Существенное превосходство	5

Построим квадратную матрицу (3.26) сравнения лингвистических конструкций:

		Неизвестная	Средне	Известная
	Неизвестная	1	3	5
SR=	Средне	1/3	1	3	(3.35)
	Известная	1/5	1/3	1

На основе применения способа 2 (3.31)-(3.33) вычисляем нормализованные оценки:

	Неизвестная	Средне	Известная
O1={	0,104729;	0,258285;	0,636986	}	(3.36)

Аналогично можно получить векторы оценок для критериев h² «Удобство доставки»,  h² «Качество обслуживания» и так далее.

В результате в формализованном виде таблица 3.1 примет вид:

Таблица 3.3

Формализованные характеристики товаров монополиста

Цена

Затраты на установку товара

Затраты на гарантию

Затраты на электро энергию

Затраты на обучение

Затраты по замене

Имидж марки компании

Удобство доставки

Качество обслужи вания

Надеж ность

Эксплуа таци онные  пока затели

Эсте тика товара

Товар1

200р.

65р.

48р.

0р.

0р.

0р.

0,105

0,896

0

0

0,599

0

Товар2

657р.

0р.

0р.

89р.

98р.

0р.

0,637

0,599

0,987

0,147

0

0

Товар3

489р.

36р.

0р.

0р.

0р.

14р.

0,258

0

0,365

0

0,987

0,47

В результате получаем, что каждый товар  имеет свой набор характеристических значений по критериям {h^y}, причем ценовые характеристики  выражаются в денежном формате, а неценовые характеристики  заданы, как лингвистические конструкции. Предложенная выше методика позволяет представить  в числовой форме.

После определения целевых аудиторий каждого из товаров и формализации неценовых параметров товара можно осуществить поиск множества оптимальных характеристик.